Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 63
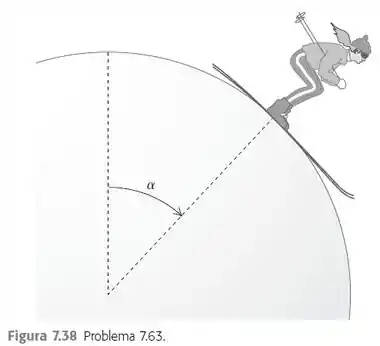
Uma esquiadora parte com velocidade inicial desprezível do topo de uma esfera de neve com raio muito grande e sem atrito, desloca-se diretamente para baixo (Figura 7.38). Em que ponto
ela perde o contato com a esfera e voa seguindo a direção da tangente? Ou seja, no momento em que ela perde o contato com a esfera, qual é o ângulo a entre a vertical e a linha que liga a
esquiadora ao centro da esfera de neve?
Passo 1
Oi, galerinha! Tudo bom? Para resolver essa questão vamos ter passar por vários conceitos físicos. Vamos com calma que está tudo descrito aqui embaixo.
O enunciado da questão é bem claro sobre o que acontece, aqui a esquiadora vai realizando um movimento circular na esfera e em determinado momento ela sai pela tangente, perde o contato com a esfera. A gente quer saber qual o ângulo formado entre o ponto inicial do movimento, e o ponto onde ela perde o contato.
Passo 2
Primeiro vamos aplicar para a esquiadora.
Repara que precisamos encontrar o ângulo onde a força normal se torna zero, em termos da velocidade neste ponto.
Em seguida, vamos aplicar o teorema da energia de trabalho ao movimento do esquiador para obter outra equação que relacione e . Resolvendo essas duas equações para o ângulo .
Vamos esboçar uma figura para essa situação do esquiador, temos que:
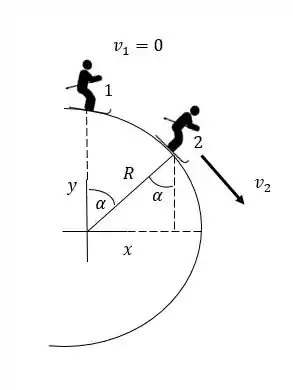
Seja o ponto 2 onde o esquiador perde contato com a bola de neve, como no esboço.
Sabemos que: perder contato implica .
Também, temos que:
e
Passo 3
Primeiro, vamos analisar as forças no esquiador quando ele estiver no ponto 2. O diagrama de corpo livre fica da seguinte forma:
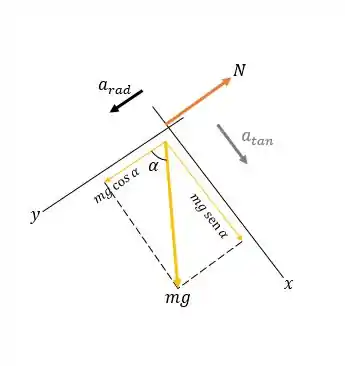
Para este usa coordenadas que estão nas direções tangencial e radial. O esquiador se move em um círculo, então sua aceleração é
Sempre direcionada para o centro da bola de neve.
Passo 4
Agora, usando a conservação de energia para obter outra equação relacionada a :
energia cinética
energia potencial gravitacional
trabalho realizado por outras forças
A única força que funciona no esquiador é a gravidade, então
Além disso, a velocidade inicial é desprezível, ou seja, .
A energia potencial pode ser calculada por:
Substituindo tudo na lei de conservação da energia:
Implica que:
Passo 5
Vamos combinar esta última equação do passo 3 com :
O que implica que:
Então,
Assim,
E por fim,
Ela acelera e seu raio aumenta à medida que perde energia potencial gravitacional. Ela perde contato quando ela está indo tão rápido que o componente radialmente interno de seu peso não é grande o suficiente para mantê-la no Caminho circular. Observe que onde ela perde contato não depende de sua massa ou do raio da bola de neve.