Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.3 - Ex. 25

Uma roda de 392 N sai do eixo de um caminhão em movimento e rola sem deslizar ao longo de uma estrada inclinada. Na base de um morro, ela está girando a 25,0 rad/s. O raio da roda é igual a 0,600 m e seu momento de inércia em torno do eixo de rotação é igual a 0,800MR2 . O atrito realiza trabalho sobre a roda à medida que ela sobe o morro até parar, a uma altura h acima da base do morro; esse trabalho possui módulo igual a 2.600 J. Calcule h.

Passo 1

E aiiiiiiiii galera, tudo bom com vocês?

Vamos fazer mais uma questão!!

Bom... o enunciado nos diz que uma roda de P = 392   N   sai do eixo de um caminhão em movimento e rola sem deslizar ao longo de uma estrada inclinada.

Na base de um morro, ela está girando a 25,0   r a d / s .

O raio da roda é igual a r = 0,600   m e seu momento de inércia em torno do eixo de rotação é igual a 0,800 M R 2 .

O atrito realiza trabalho sobre a roda à medida que ela sobe o morro até parar, a uma altura h acima da base do morro; esse trabalho possui módulo igual a 2.600   J .

Queremos calcular a altura h .

Para isso, vamos usar a conservação de energia!!

Passo 2

Bom... A roda tinha inicialmente energias cinéticas rotacional K E r e transicional K E t .

Em seguida, o atrito realizou um trabalho W f e a roda parou na altura h , onde há uma energia potencial gravitacional P E .

Assim, temos:

K E r + K E t - W f = P E ∴

1 2 I ω 0 2 + 1 2 M v 0 2 - W f = M g h

Onde I é o momento de inércia, ω 0 é a velocidade angular inicial, M g é o peso P da roda, M é a massa da roda, v 0 é a velocidade inicial da roda e g é a aceleração da gravidade.

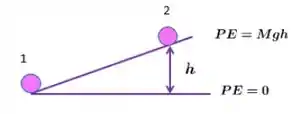
Abaixo, podemos ver o esquema do problema:

Passo 3

Usando   ( v 0 = ω 0 R ,  e  I = 0.8 M R 2 , temos:

0.8 1 2 M R 2 ω 0 2 + 1 2 M ω 0 2 R 2 - W f = M g h

Como M = W g , podemos substituir os valores:

h = ( 0.8 ) 1 2 392 9.8 ( 0.6 ) 2 ( 25 ) 2 + 1 2 392 9.8 ( 25 ) 2 ( 0.6 ) 2 - 2600 392

h = 14 m

Resposta

h = 14 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma massa pontual de 0,20k g se movendo em uma superfície horizontal sem atrito está preso a uma tira elástica que tem a outra extremidade fixa no ponto P . A tira elástica exerce uma força de magnitu
A figura mostra um cilindro oco de 1,80 m de comprimento e 0,80 k g de massa, com raio igual a 0,20 m . O cilindro pode girar em torno de um eixo vertical que passa perpendicularmente pelo seu centro.
A figura mostra um tubo cilindro oco de massa M , comprimento L e momento de inércia M L 2 / 10 . Dentro do cilindro há dois discos, cada um de massa m e raio r , separados por uma distância l e amarr
Um interessante fenômeno que ocorre em certos pulsares (veja o problema 24) é o evento conhecido como “pane de spin”, isto é, uma rápida mudança na taxa de spin do pulsar, devida a uma redistribuição
Considere uma plataforma giratória cilíndrica de massa M e raio R , girando com uma rapidez angular inicial ω 1 . (a) Um periquito de massa m , após esvoaçar acima da plataforma, pousa suavamente sobr