Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 69
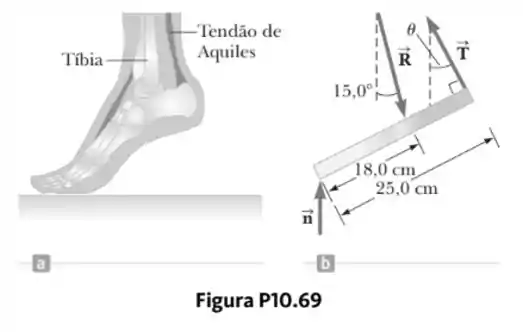
Quando uma pessoa fica na ponta de um pé (uma posição difícil), a posição do pé é como mostrada na Figura P10.69a. A força gravitacional total no corpo é suportada pela força normal exercida pelo chão sobre os dedos de um pé. Um modelo mecânico da situação é mostrado na Figura P10.69b, onde é a força exercida no pé pelo tendão de Aquiles e é a força exercida no pé pela tíbia. Encontre os valores de , e quando .
69
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Observe que a força R (exercida no pé pela tíbia) foi substituída pela suas componentes horizontal e vertical. Empregando ambas as condições de equilíbrio (usando o ponto O como o ponto de pivô) temos as três seguintes equações:
Passo 2
Substituindo a equação [3] na equação [1] temos:
Substituindo as equações [3] e [4] na equação [2] temos:
Elevando ao quadrado este resultado e usando , temos:
Neste último resultado, seja e avalie as constantes para obter a equação quadrática:
As soluções são , então:
Passo 3
Vamos ignorar a inclinação 83.8 porque é humanamente impossível, então
Então, da equação [3]:
E da equação [1]: