Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 41.Problemas - Ex. 43
a) Para um estado excitado do átomo de hidrogênio, mostre que o menor ângulo que o momento angular orbital pode formar com o eixo é dado por
b) Qual é a expressão correspondente do maior ângulo que o momento angular orbital pode formar com o eixo ?
Passo 1
Primeiramente podemos utilizar a figura:
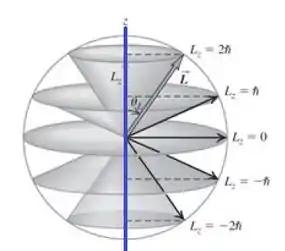
para relacionar com , o que nos da:
Passo 2
a) Queremos mostrar o resultado no qual é mínimo e quando isso acontece teremos o maior e o maior . Então:
Sabemos que o momento angular em é:
Já o momento angular é:
Mas no passo 1 já vimos quais as relações entre , agora só basta aplicarmos as condições para ser mínimo:
Passo 3
b) O maior ângulo que pode ser formado com o eixo , ou seja, acontece quando:
e
Portanto o é:
Resposta
a)
b)
Exercícios de Livros Relacionados
Um átomo de Rydberg é aquele cujos elétrons da camada externa estão em um estado excitado com numero quântico principal muito grande. Os átomos de Rydberg foram produzidos em laboratório e também dete
A função de onda para o átomo de hidrogênio no estado 2 s é dada por ψ 2 s r = 1 32 π a 3 2 - r a e - r 2 a a) Mostre que essa função de onda é normalizada. b) no modelo de Bohr, a distância entre o e
O princípio de exclusão de Pauli afirma que não mais que um elétron pode ocupar um estado quântico particular de cada vez. Os elétrons ocupam intrinsecamente dois estados de rotação. Portanto, se dese