Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 3.Problemas - Ex. 76
Um estilingue lança uma pequena pedra do solo com velocidade v0, a um ângulo u0 acima do solo. Você precisa determinar v0. Pela forma como o estilingue foi construído, você sabe que, para uma boa aproximação, v0 é independente do ângulo de lançamento. Você vai até um campo aberto e nivelado, seleciona um ângulo de lançamento e mede a distância horizontal que a pedra percorre. Você usa g 9,80 m/s2 e despreza a pequena altura da ponta do estilingue acima do solo. Como sua medição inclui alguma incerteza nos valores medidos para o ângulo de lançamento e para o alcance horizontal, você repete a medição para diversos ângulos de lançamento e obtém os resultados dados na Figura P3.76. A resistência do ar é desprezada, pois não há vento e a pedra é pequena e pesada. (a) Selecione um modo de representar os dados como uma linha reta. (b) Use a inclinação da linha com melhor ajuste de seus dados do item (a) para calcular v0. (c) Quando o ângulo de lançamento é 36,9º, qual é a altura máxima que a pedra alcança acima do solo?
Passo 1
Você tem um gráfico que mostra a extensão horizontal da rocha em função do ângulo em que foi lançado e deseja encontrar sua velocidade inicial. Como a resistência do ar é insignificante, a pedra está em queda livre. A fórmula de intervalo aplica-se desde que a pedra foi lançada do solo e cai no solo.
Letra a:
A fórmula do intervalo é:
portanto, um gráfico de R versus dará uma linha reta tendo inclinação igual a Podemos usar esses dados no gráfico do problema para construir nosso gráfico.
O gráfico resultante é mostrado na figura:
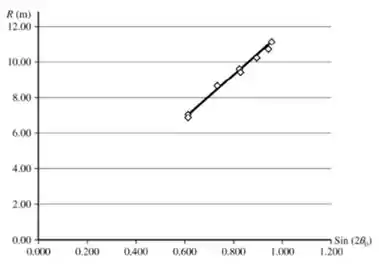
Passo 2
Letra b:
A inclinação do gráfico é 10,95m, então . Resolvendo para , temos
Passo 3
Letra c:
Resolvendo a fórmula no ponto mais alto, nós temos
Esta abordagem para encontrar a velocidade de lançamento requer apenas medições simples: o alcance e o ângulo de lançamento. Seria difícil e exigiria equipamento especial para medir diretamente.
Resposta
- Ver gráfico