Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 15
Estime o valor da capacitância da garrafa de Leyden mostrada na Figura. A figura do homem tem um décimo da altura média de um homem.
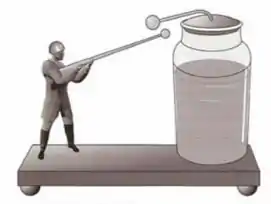
Passo 1
Cara... Exercício doido, neh?
Mas fazendo uma busca rápida na internet, descobrimos que um capacitor de Leyden pode ser considerado com um capacitor cilíndrico entre uma placa de carga no interior do vidro e outra fora dele...
Onde é o raio do pode do cilindro e é o valor do raio do cilindro incluindo a espessura do vidro que separa uma placa de carga da outra. No geral, para uma garrafa simples normal, e .
Layden, ainda fala pra gente que a capacitância de um capacitor de Layden pode ser considerada então como a capacitância desse capacitor cilíndrico, ou seja, que...
Então veja que podemos estivar o valor da capacitância de Layden conhecendo a altura do pote (), já que e vamos considerar como sendo os valores típicos de um pote de maionese ( e ).
Passo 2
Ora... Não conhecemos diretamente a altura da garrafa, mas sabemos que o boneco perto dela...
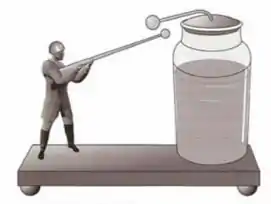
Mede um décimo da altura média de um homem. Se considerarmos que em média um homem brasileiro tem (ou estou muito abaixo da média rsrsrs), então, a altura média do boneco será...
Vamos então considerar que essa também é a altura do pote, ta legal?
Passo 3
Então com isso. Podemos estimar a capacitância dessa garrafa de Layden...
Como ...
Então a capacitância do pote será de aproximadamente...
E como é a ordem ...