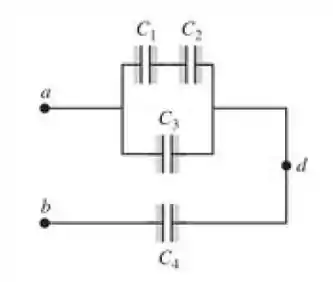
Na figura abaixo, cada capacitor possui e .Calcule (a) a carga de cada capacitor; (b) a diferença de potencial através de cada capacitor; (c) a diferença de potencial entre os pontos a e d.

letra a)

Queremos a carga de cada capacitor.

Sabemos que capacitores em série tem a mesma carga, logo:

Além disso sabemos que o potencial de capacitores em paralelo é:

E que a diferença de potencial total será:

Pegando a relação dos potenciais

E substituindo e pela fórmula com a capacitância, temos:

Vamos guardar essa equação!!!!

Sabemos também que a diferença de potencial total está relacionada com a capacitância equivalente.

E como já vimos :

Precisamos então determinar .

Os capacitores e estão em série, logo:

Os capacitores e estão em paralelo, logo:

Os capacitores e estão em série, logo:

Podemos agora achar :

Podemos agora achar :

Precisamos achar agora e .

Eles estão em série, então .

Além disso:

Se substituirmos as diferenças de potencial, teremos:

Logo:

letra b)

Agora precisamos calcular todos os potenciais.

Como sabemos as cargas dos capacitores e as capacitâncias:

Para o capacitor 1:

Para o capacitor 2:

Para o capacitor 3:

Para o capacitor 4:

letra c)

Para acharmos o potencial entre os pontos a e d, precisamos achar a capacitância e a carga equivalente entre os capacitores 1, 2 e 3.

A capacitância equivalente, já foi calculada no passo 6:

Agora precisamos da carga equivalente, como e estão em série:

E como está em paralelo com :

Agora calculamos o potencial entre a e d: