Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 70
Uma estudante pretende determinar os coeficientes de atrito estático e atrito cinético entre uma caixa e uma tábua. Para isso, coloca a caixa sobre a tábua e levanta lentamente uma das extremidades da tábua. Quando o ângulo de inclinação em relação à horizontal chega a , a caixa começa a escorregar e percorre ao longo da tábua em , com aceleração constante. Quais são (a) o coeficiente de atrito estático e (b) o coeficiente de atrito cinético entre a caixa e a tábua?
Passo 1
a) Oláaaa, querido! Então, a menina colocou o bloco sobre a mesa e inclinou a mesa. No ângulo de o bloco começa a deslizar.
Aí ele quer o coeficiente de atrito estático da mesa.
Vamos pensar na situação onde há eminência de movimento. Imediatamente antes do bloco começar a deslizar. Podemos dizer que o ângulo onde isso acontece é esse ângulo de .
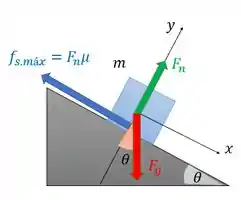
Na eminência do movimento, temos que a força de atrito estática é máxima e vale:
Iremos aplicar a segunda lei de Newton para o eixo e o eixo para achar .
Passo 2
De acordo com a 2° Lei de Newton no eixo x para o bloco, vamos ter
Como estamos em equilíbrio, , então:
Aí nessa direção, a gente temos , no sentido negativo se opondo a tendência de movimento. E temos também a componente de que é dada por que aponta para positivo.
O somatório de forças fica
Agora a segunda lei de Newton para esse mesmo bloco para a direção , sabendo que :
Nessa direção temos a força normal para a parte positiva e a componente de para baixo. O somatório fica:
Dividindo a equação pela :
Passo 3
b) Nos queremos o coeficiente de atrito cinético.
Ou seja, estamos no momento onde não é mais nula e o bloco se move. Ele forneceu alguns dados, para que possamos encontrar a mesma. Ele diz que o bloco sai do repouso , e anda em . Para achar , podemos usar essa equação para aceleração constante:
Agora a gente vai aplicar a segunda lei de Newton para esse novo momento e achar . Nosso diagrama fica:
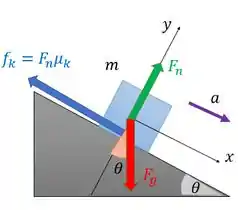
Bora lá!
Passo 4
De acordo com a 2° Lei de Newton no eixo x para o bloco, vamos ter
Aí nessa direção, a gente temos , no sentido negativo se opondo ao movimento. E temos também a componente de que é dada por que aponta para positivo.
O somatório de forças fica
Agora a segunda lei de Newton para esse mesmo bloco para a direção , sabendo que :
Nessa direção temos a força normal para a parte positiva e a componente de para baixo. O somatório fica:
Substitindo em :
Substituindo os valores
Resposta
De boa pessoal???? Bora resolver mais questões então!!!!!