Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 88

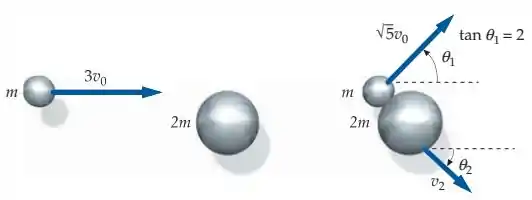
A figura mostra o resultado de uma colisão entre dois corpos de massas desiguais. (a) Determine a rapidez v 2 da massa maior após a colisão; encontre, também, o ângulo θ 2 . (b) Mostre que a colisão é elástica.

Passo 1

Mais uma questãozinha de colisões. Vamos querer o de sempre, usar quantidade de movimento e conservação de energia.

Passo 2

  1. Conservação da quantidade de movimento no eixo x:

    2. m × 3 v 0 = m × v 0 5 c o s θ 1 + 2 m v 2 c o s θ 2

    3 v 0 = v 0 5 c o s θ 1 + 2 v 2 c o s θ 2

    Conservação da quantidade de movimento no eixo y:

    m v 0 5 s e n θ 1 = 2 m v 2 s e n θ 2

    v 0 5 s e n θ 1 = 2 v 2 s e n θ 2

    Ele falou que t a n θ 1 = 2 . Vamos usar isso pra achar os valores do seno e do cosseno.

    t a n θ 1 = s e n θ 1 c o s θ 1 = 2 → s e n θ 1 = 2 c o s θ 1

    Usando a relação fundamental:

    s e n 2 θ 1 + θ 1   = 1

    2 c o s θ 1 2 + θ 1   = 1

    θ 1   = 1 5 → c o s θ 1 = 5 5 → s e n θ 1 = 2 5 5

    Agora podemos substituir nas expressões encontradas ali em cima:

    Passo 3

    v 0 5 c o s θ 1 + 2 v 2 c o s θ 2 = 3 v 0

    v 0 5 × 5 5 + 2 v 2 c o s θ 2 = 3 v 0

    v 0 + 2 v 2 c o s θ 2 = 3 v 0

    v 2 c o s θ 2 = v 0   ( * )

    v 0 5 × 2 5 5 = 2 v 2 s e n θ 2

    2 v 0 = 2 v 2 s e n θ 2

    v 2 s e n θ 2 = v 0   ( * * )

    Das equações * e * * :

    s e n θ 2 = c o s θ 2

    θ 2 = 45 °

    Botando lá na equação: v 2 s e n 45 ° = v 0 → v 2 = v 0 2 .

    Passo 4

  2. Agora vamos fazer a conta da energia:

K i = m 3 v 0 2 2 = 9 m v 0 2 2

K f = m 5 v 0 2 2 + 2 m 2 v 0 2 2 = 9 m v 0 2 2

Como a energia se conservou, a colisão é elástica.

Resposta

  1. v 2 = 2 v 0 , θ 2 = 45 °
  2. A colisão é elástica.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula de velocidade v 0 colide elasticamente com outra idêntica em repouso. No referencial do CM, a direção de movimento é desviada de 60 ° em virtude da colisão. Calcule os ângulos de deflexã
Uma partícula de massa m desloca-se com velocidade v em direção a duas outras idênticas, de alinhadas com ela, inicialmente separadas e em repouso (veja fig.). As colisões entre as partículas são toda
Uma partícula de massa m e velocidade inicial u colide elasticamente com outra de massa M , inicialmente em repouso no referencial de laboratório. Após a colisão, a partícula de massa m foi defletida
Um cavaleiro de 0,150k g move-se a 0,80m / s da esquerda para a direita sobre um trilho de ar horizontal sem atrito. Ele colide frontalmente com um cavaleiro de 0,300k g que se move a 2,20m / s da dir
Você está controlando um acelerador de partículas, enviando um feixe de 1 , 50 . 10 7m / s de prótons (de massa m ) sobre um alvo gasoso de um elemento desconhecido. Seu detector mostra que alguns pró