Uma partícula tem uma rapidez inicial . Ela colide com uma segunda partícula de mesma massa, que está inicialmente em repouso. A primeira partícula é defletida de um ângulo . Sua rapidez, após a colisão, é . A segunda partícula recua e sua velocidade forma um ângulo com a orientação original da primeira partícula. (a) Mostre que . (b) Mostre que, se a colisão é elástica, então .
Passo 1
A situação vai ser a seguinte:
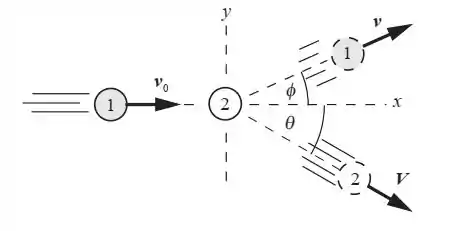
Como em toda questão de colisões, vamos usar de cara a quantidade de movimento:
Passo 2
No eixo x:
No eixo y:
Dividindo a segunda equação pela primeira:
Passo 3
Ele diz que a colisão é elástica. Logo, a energia se conserva:
Tá vendo que isso é equivalente ao teorema de Pitagoras? Então podemos então representar os vetores assim, já que vale o teorema de Pitágoras:
Além disso, essa representação é válida pela conservação de movimento (vetorial):
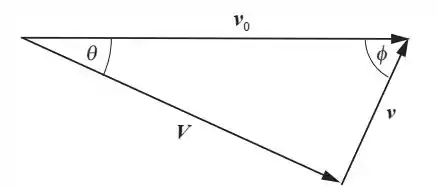
Daqui, tiramos que .
Resposta
Ei, a resposta está no passo a passo :)