1. Vamos observar a situação pra facilitar o raciocínio, chega junto

• Situação inicial



• Situação final



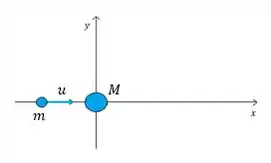
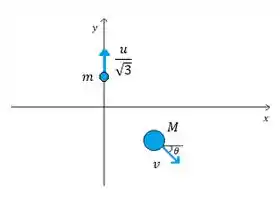
Também se liga como fica a conservação do momento linear do sistema desenhada



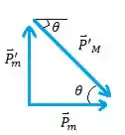
Assim, podemos escrever

Portanto nosso ângulo é o arco cuja tangente é , ou seja,

Passo 2

• Olhando para nosso triângulo com os momentos vamos ver que

Agora, como a colisão é elástica, pela conservação da energia cinética

Em função dos momentos lineares as energias cinéticas se tornam

Usando , como pedido no enunciado fica assim ó

Substituindo os momentos iniciais e finais da partícula de massa , nossa equação se torna

Finalmente, obtemos as razões entre as massas

Agora, pra achar é só usar nossa equação inical de novo

Passo 3

• Agora que sabemos as razões entre as masssa vamos escrever

Galera, aqui o nosso vetor velocidade está na direção positiva do eixo x, por isso fica assim

Pelo nosso esqueminha da situação final lá em cima vemos que a massa vai na direção do eixo y e por isso sua velocidade relativa em relação ao centro de massa é dada por

Para calcular o ângulo desse vetor com relação ao centro de massa vamos usar o produto escalar

Como a gente quer cular o ângulo entre os vetores “velocidade relativa ao centro de massa” e “velocidade do centro de massa” temos o seguinte,

Show! Já temos quase tudo, só falta calcular o produto escalar. Vem comigo!

Como , nosso produto se torna

Finalmente, aplicando a propriedade do produto escalar fica assim

Passo 4

Fazendo a mesma coisa para descobrir vamos escrever , que faz com a horizontal

Para a velocidade relativa temos

Agora só falta juntar tudo e descobrir o coseno, desse jeito