Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 48

Um grande espelho é pendurado em um prego, como mostrado na figura 12-47. O fio de aço que o suporta tem um diâmetro de 0,20   m m e comprimento não alongado de 1,7   m . A distância entre os pontos de suporte na parte superior da moldura do espelho é 1,5   m . A massa do espelho é 2,4   k g . De quanto aumentará a distancia entre o prego e o espelho, devido à elongaçõa sofrida pelo fio, quando o espelho é pendurado?

Passo 1

Primeiramente, vamos fazer uma ilustração pra entender melhor o que ta acontecendo!

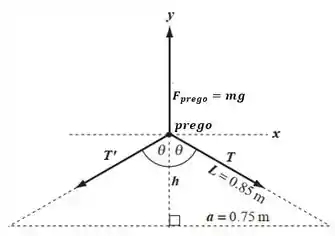
Fazendo um Pitágoras no tringulo acima:

a 2 + h 2 = L 2

Derivando, temos:

2 h   d h = 2 L   d L → h d h = L d L

Pois nosso a é constante!

Passo 2

Lá do módulo de Young, sabemos o seguinte:

Y = F / A Δ L / L

Logo,

Δ L = T L A Y   ( i )

Vamos fazer a seguinte aproximação, pois temos variações pequenas:

h d h = L d L → h Δ h = L Δ L

Como queremos saber Δ h :

Δ h = L Δ L h

Usando ( i ) :

Δ h = L 2 h ⋅ T A Y

Considerando a seção do fio circular:

A = π r 2

Então,

Δ h = L 2 h ⋅ T π r 2 Y     ( i i )

Passo 3

Pra finalizar, precisamos achar a tração. No eixo y vamos ter o seguinte.

∑ F y = 0

Logo,

m g - 2 T c o s θ = 0 → T = m g 2 cos ⁡ θ = m g 2 ⋅ L L 2 - a 2

Substituindo em ( i i ) :

Δ h = L 2 L 2 - a 2 ⋅ m g 2 ⋅ L L 2 - a 2 π r 2 Y

Arrumando essa coisa feia:

Δ h = L 3 L 2 - a 2 ⋅ m g 2 π r 2 Y

Substituindo os valores:

Δ h = 0,85   m 3 0,85   m 2 - 0,75   m 2 ⋅ 2,4   k g ⋅ 9,81 N k g 2 π ⋅ 0,1 × 10 - 3   m 2 ⋅ 2,00 × 10 11 N m 2

Fazendo esse tanto de conta:

Δ h = 7,2   m m

Resposta

Δ h = 7,2   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma tora homogênea , de 100 k g de massa, 4,0m de comprimento e 12c m de raio, é mantida em uma posição inclinada como mostrado na Figura 12-44. O coeficiente de atrito estático entre a tora e a super
Duas massas, M 1 e M 2 , estão suspensas por fios que têm comprimento iguais quando frouxos. O fio que suporta M 1 é de alumínio e tem 0,70m m de diâmetro, e o que suporta M 2 é de aço e tem 0,50m m d
Se a massa específica de um material permanece constante quando alongado em uma direção, então (porque seu volume total permanece constante) seu comprimento, em uma ou nas duas outras direções, deve d
O cabo de um elevador deve ser feito com um novo tipo de composto. No laboratório, uma amostra do cabo, com 2,00m de comprimento e uma área de seção reta de 0,200m m 2 , se rompe com uma carga de 1000
Uma bola de 0,50k g é presa a uma extremidade de um fio de alumínio que tem um diâmetro de 1,6m m e um comprimento não distendido de 0,70m . A outra extremidade do fio está fixa em cima de um poste. A