Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 11.Problemas - Ex. 90
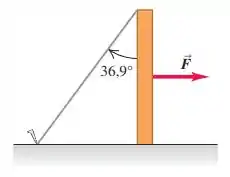
A extremidade de um poste que pesa 400 N e de altura h está apoiada sobre uma superfície horizontal com μs 0,30. A extremidade superior do poste está sustentada por uma corda amarrada à superfície horizontal e fazendo um ângulo de 36,9° com o poste (Figura P11.90). Uma força horizontal é aplicada sobre o poste conforme indicado. (a) Quando a força é aplicada em seu centro, qual deve ser seu módulo máximo para que o poste não comece a deslizar? (b) Se o ponto de aplicação da força está situado a seis décimos da altura do poste a partir de sua base, qual deve ser o módulo máximo da força para que o poste não comece a deslizar? (c) Mostre que, se o ponto de aplicação da força estiver situado em um ponto muito elevado, o poste não poderá deslizar, por maior que seja o módulo da força. Ache a altura crítica para o ponto de aplicação dessa força.
Passo 1
E aiiiiiiiii galera, tudo bom com vocês?
Vamos fazer mais uma questão!!
Bom... o enunciado nos diz que a extremidade de um poste que pesa e de altura está apoiada sobre uma superfície horizontal com coeficiente de atrito estático , conforme a figura:
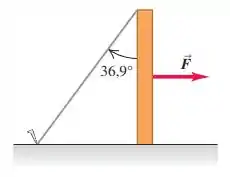
A extremidade superior do poste está sustentada por uma corda amarrada à superfície horizontal e fazendo um ângulo de com o poste.
Uma força horizontal é aplicada sobre o poste conforme indicado.
Queremos calcular na letra (a) o módulo máximo da força de forma que o poste não comece a deslizar.
Na letra (b) a gente vai faze a mesma coisa, mas com seis décimos da altura do poste a partir de sua base.
Por fim, na letra (c), queremos mostrar que, se o ponto de aplicação da força estiver situado em um ponto muito elevado, o poste não poderá deslizar, por maior que seja o módulo da força.
Passo 2
Letra a:
Abaixo temos o diagrama de corpo livre:
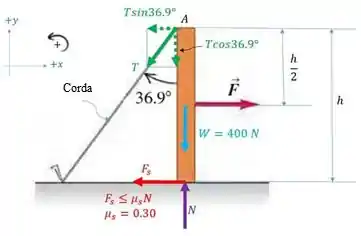
E agora, vamos equacionar:
Para
Onde é a tensão da corda, é a normal, é a força peso e é a força de atrito.
Passo 3
Para
Para
Aplicando a equação :
Passo 4
Substituindo os valores, temos:
Dessa forma, a força é:
A magnitude máxima de F é 400 N sem o deslizamento do poste.
Passo 5
Letra b:
Abaixo, o diagrama de corpo livre para o poste, só que com outras variáveis de altura.
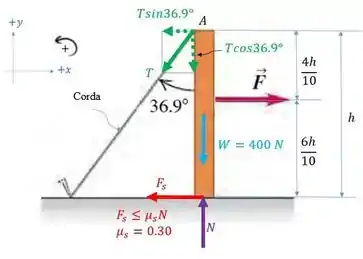
Sabemos que:
Logo:
Vamos chamar de equação .
Passo 6
De forma análoga a letra (a), vamos verificar as forças na horizontal:
Aplicando a equação , temos:
Vamos chamar de equação .
Passo 7
Agora para as forças na vertical, temos:
Aplicando a equação :
A magnitude máxima de é sem que o poste escorregue.
Passo 8
Letra c:
Olhando o diagrama de corpo livre da questão anterior, substituindo as alturas de e por h-y e y, respectivamente, temos:
Vamos chamar de equação .
Passo 9
Analisando as forças na horizontal, temos:
Aplicando a equação , temos:
Vamos chamar de equação .
Passo 10
Pelas forças na vertical, temos:
Aplicando a equação , temos:
Portanto:
Caso o denominador do termo entre parênteses seja zero, o limite para seria o infinito.
Passo 11
A altura crítica é fornecida quando o denominador da expressão acima entre parênteses é zero:
Resposta
- A magnitude máxima de é sem o deslizamento do poste.
- A magnitude máxima de F é sem que o poste escorregue.