Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 22
Qual é a distancia máxima que um homem de massa pode subir ao longo do Probl. 21, sem que a escado escorregue
Passo 1
Essa questão é bem parecida com a questão 20, se liga só:
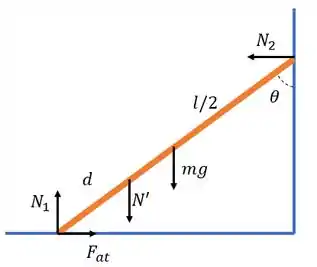
Como o sistema está em equilíbrio:
Logo,
Mas esse é a reação do peso do homem na barro, logo:
Para o eixo :
Assim,
Mas a gente sabe que .
Passo 2
Agora que já garantimos que , basta fazermos . Considerando positivo no sentido horário:
Arrumando as coisas:
Então,
Como g:
Assim,
Portanto, o maior valor de será:
Resposta
Exercícios de Livros Relacionados
Um lápis sextavado é colocado sobre um caderno (Figura 12-53). Determine o menor coeficiente de atrito, tal que, se a capa do caderno for erguida, o lápis rolará para baixo sem escorregar.
Um a caixa de 8,0 kg, de massa específica uniforme e duas vezes mais alta do que larga, é colocado sobre o piso de um caminhão. Qual é o maior coeficiente de atrito estático entre a caixa e o piso, ta
Um cubo está apoiado em uma parede sem atrito, formando um ângulo θ com o chão, como mostrado na Figura 12-55. Determine o menor coeficiente de atrito estático entre o cubo e o chão, necessário para e
A Figura 12-57 mostra uma escada de 20,0 kg apoiada em uma parede sem atrito e sobre uma superfície horizontal sem atrito. Para evitar que a escada escorregue, sua base é amarrada à parede com um aram
Uma escada homogênea está apoiada contra uma parede vertical sem atrito. O coeficiente de atrito estático entre a escada e o piso é 0,30 . Qual é o menor ângulo entre a escada e a horizontal para que