Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas adicionais - Ex. 123
Uma das extremidades de uma barra longa, de vidro (), é uma superfície convexa com de raio. Um objeto está situado no ar, no prolongamento do eixo da barra, a de distância da extremidade convexa. (a) Qual é a distância entre o objeto e a imagem formada pela barra de vidro? (b) Qual é o intervalo de distâncias entre o objeto e a extremidade da barra no qual o objeto deve ser colocado para que seja produzida uma imagem virtual?
Passo 1
Fala galerinha, beleza?
Prontos para mais uma questão de ótica?
O primeiro passo nesse problema é encontrar o foco da lente biconvexa:
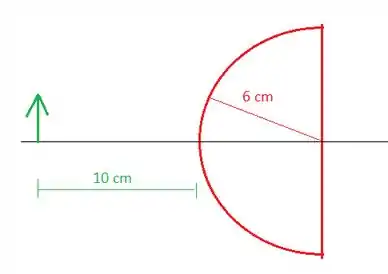
Para isso, usamos a expressão
Nesse caso, e . Com isso, temos que
Portanto,
Passo 2
Agora que temos o foco, vamos achar a posição da imagem:
Logo,
Assim,
Portanto,
Passo 3
Para que a imagem seja virtual, devemos ter , de modo que
Assim,
Assim, para que a imagem seja virtual, devemos ter