Em uma fábrica, caixotes de são deixados cair verticalmente de uma máquina de empacotamento em uma esteira transportadora que se move a (Fig. 8-62). (A velocidade da esteira é mantida constante por um motor.) O coeficiente de atrito cinético entre a esteira e cada caixote é . Após um pequeno intervalo de tempo, deixa de haver deslizamento entre a esteira e o caixote, que passa a se mover com a mesma velocidade que a esteira. Para o intervalo de tempo no qual o caixote está deslizando sobre a esteira, calcule, tomando como referência um sistema de coordenadas em repouso em relação à fábrica, (a) a energia cinética total fornecida ao caixote, (b) o módulo da força de atrito cinético que age sobre o caixote e (c) a energia total fornecida pelo motor. (d) Explique por que as respostas dos itens (a) e (c) são diferentes.

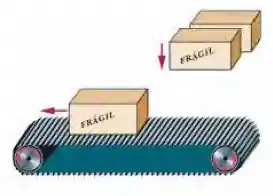
Figura 8-62 Problema 78

b) A força de atrito cinético é dado por

Para e

c) Seja a distância percorrida pelo caixote. Pela equação de Torricelli

Como

E temos que

Logo

A variação da energia térmica será

E a energia total fornecida

d) A energia fornecida pelo motor é maior pois parte dela é dissipada na forma de calor ().