Um feixe de luz que contém todos os comprimentos de onda entre e incide perpendicularmente em uma rede de difração com . (a) Qual é a menor ordem que se superpõe a outra ordem? (b) Qual é a maior ordem para a qual todos os comprimentos de onda do feixe original estão presentes? Nessa ordem, determine para que ângulo é observada a luz (c) de e (d) de . (e) Qual é o maior ângulo para o qual a luz de aparece?

(a) Primeiro calculamos a distância entre as ranhuras. Já que temos ranhuras a cada milimetro, a distância (em metros) é:

E então, para e , temos o seguinte:

E agora se continuarmos com isso para outros valores (e analisando os dois extremos da faixa de comprimentos de onda), vamos encontrar os seguintes dados:

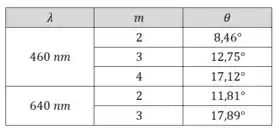
Com isso, vemos que a menor ordem que se superpõe a outra é a terceira (, ), que se superpõe à quarta ().

(b) Agora queremos saber qual é a maior ordem que “inclui” todos os comprimentos de onda presentes?

Vamos dar uma olhada na fórmula para as posições dos máximos:

Como , podemos escrever o seguinte:

Isso quer dizer que quanto maior for , mais limitado estará o nosso . No caso em que (o maior valor presente no feixe):

Ou seja, a maior ordem para a qual todos os comprimentos de onda estão presentes é .

(c) Agora vamos calcular a posição angular dessa mesma ordem para o comprimento de onda :

(d) E temos que fazer a mesma coisa para :

(e) Queremos saber qual é o maior valor que assume para o comprimento de onda .

Vamos lembrar da condição que escrevemos lá em cima usando o fato de que :

Isso quer dizer que podemos ter, no máximo . Qual é o valor de nesse caso?