Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.1 - Ex. 9

Uma fenda com 1,00 mm de largura é iluminada com uma luz cujo comprimento de onda é 589 nm. Uma figura de difração é observada em uma tela situada a 3,00 m de distância da fenda. Qual é a distância entre os primeiros dois mínimos de difração situados do mesmo lado do máximo central?

Passo 1

Nesse exercício vamos utilizar a equação para o mínimo de difração e as relações trigonométricas para estabelecer conexões entre a distância do máximo central e o primeiro e segundo mínimo.

Passo 2

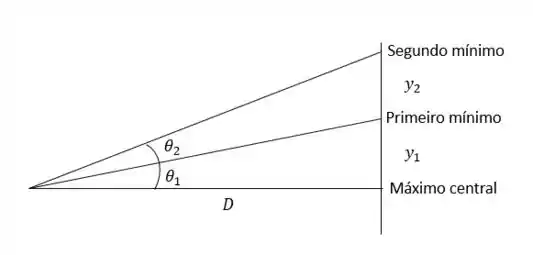
Temos que para encontrarmos as distâncias y 1 e y 2 precisaremos encontrar primeiro os ângulos para cada mínimo da difração. Podemos usar para encontrar esses ângulos a relação a ⋅ sin ⁡ θ = m ⋅ λ . Assim, se manipularmos a relação, chegamos que o ângulo pode ser encontrado por

θ 1 = sin - 1 ⁡ m 1 ⋅ λ a

θ 2 = sin - 1 ⁡ m 2 ⋅ λ a

Como queremos o ângulo do primeiro e do segundo mínimo, temos que m 1 = 1 e m 2 = 2 . Logo, substituindo na equação, chegamos que

θ 1 = sin - 1 ⁡ 589 × 10 - 9   m 1,00 × 10 - 3   m = 0,034 º

θ 2 = sin - 1 ⁡ 2 ⋅ 589 × 10 - 9   m 1,00 × 10 - 3   m = 0,067 º

Passo 3

Agora para encontrarmos y 1 e y 2 , podemos estabelecer uma relação trigonométrica dada por

tan ⁡ θ = y 1 D

Assim, ficamos que

y 1 = D ⋅ tan ⁡ θ 1

y 2 = D ⋅ tan ⁡ θ 2

Substituindo os valores de θ e de D , chegamos que

y 1 = 3,00   m ⋅ tan ⁡ 0,034 º = 1,78 × 10 - 3 m

y 2 = 3,00   m ⋅ tan ⁡ 0,067 º = 3,50 × 10 - 3 m

Passo 4

Agora basta calcularmos a diferença entre y 1 e y 2 e teremos a distância entre os mínimos. Assim:

Δ y = y 2 - y 1 = 3,50 × 10 - 3   m - 1,78 × 10 - 3   m = 1,72 × 10 - 3   m

Resposta

Δ y = 1,72 × 10 - 3   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A luz de um laser de comprimento de onda 632,8n m incide normalmente em uma fenda com 0,0250m m de largura. A luz transmitida é vista sobre uma tela distante onde a intensidade no centro da franja bri
1. Uma onda plana monocromática incide perpendicularmente sobre um anteparo opaco com beirada retilínea, projetando sua sombra sobre outro anteparo, paralelo ao primeiro, e situado dentro da região de
3. A construção sobre um plano Σ das zonas de Fresnel pode ser estendida a uma onda incidente esférica, proveniente de um ponto fonte F (fig.). Nesse caso, o pólo O se obtém unindo o ponto de observaç
4. Considere a função f X = sen 2 ⁡ X / X 2 (figura de difração de uma fenda). Mostre que os máximos secundários são raízes da equação tg ⁡ X n = X n e procure determinar os seus valores, bem como os
Um padrao de difracao de fenda simpleseformado usando luz de laser monocromatico com comprimento de onda de 450 nm. Oque acontece com a distancia entre o primeiro maximo e o maximo central quando a la