Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 4.Problemas - Ex. 4
4. Considere a função (figura de difração de uma fenda). Mostre que os máximos secundários são raízes da equação e procure determinar os seus valores, bem como os de , para usando métodos gráficos ou numéricos (calculadora).
Passo 1
Vem comigo que não vai ter problema que não podemos resolver.
Para demonstrar o que o enunciado pede vamos usar nosso conhecimento de calculo sobre como encontrar os pontos que extremos de uma função ocorre, que são os pontos que fazem a primeira derivada zerar.
Vamos aplicar isso na função e ver se os valores de que fazem a derivada dessa função ser zero são raízes de .
Ah não se preocupe com esse o é só para indicar que raiz estamos nos referindo.
Antes de começarmos, um detalhe que vai ser importante é que a função tem seus mínimos em (para diferente de zero).
Vamos lá então!
Passo 2
Vamos começar derivando , temos:
E isso que encontramos tem que ser igual a zero.
Como não estamos considerando o caso de já que é onde ocorre o máximo principal, temos:
Passo 3
Como eu disse no passo os mínimos só ocorrem em , e a expressão que encontramos só zera para esse valor de por conta do fatorado.
Então se liga no seguinte, não queremos que esse seno seja zero, então podemos dividir nossa expressão por nós não teremos mais os casos dos mínimos, então os valores de que zeram
São os que vão nos dar os máximos.
Concorda comigo que nada nos impede de dividir os dois lados por , então:
Então os valores que zeram essa expressão que encontramos também zera a expressão anterior que tínhamos. Prontinho demonstramos os que o enunciado pedia.
Passo 4
Abaixo temos uma figura com o gráfico das duas funções,
e
e você pode reparar que pelo menos nos primeiros valores das funções que a a primeira zera no mesmo ponto onde a segunda tem um máximo secundário.
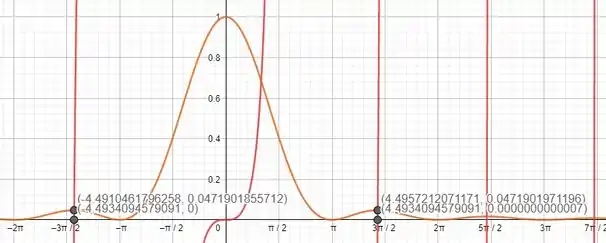
Você pode reparar que os valores diferem na terceira casa decimal, mas isso é porque não estamos lidando com valores exatos, mas na prática elas zeram.
Resposta
Demonstrado acima.