Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.1 - Ex. 10
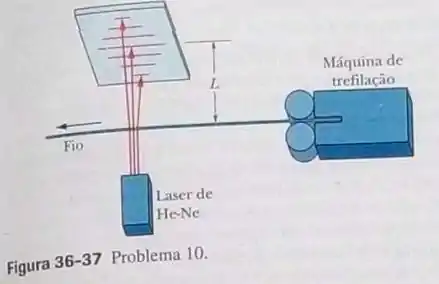
Os fabricantes de fios (e outros objetos de pequenas dimensões) às vezes usam um laser para monitorar continuamente a espessura do produto. O fio intercepta a luz do laser, produzindo uma figura de difração parecida com a de uma fenda com a mesma largura que o diâmetro do fio (Fig. 36-37). Suponha que o fio seja iluminado com um laser de hélio-neônio, com um comprimento de onda de 632,8 nm, e que a figura de difração apareça em uma tela situada a uma distância do fio. Se o diâmetro do fio é 1,37 mm, qual será a distância observada entre dois mínimos de décima ordem (um de cada lado do máximo central)?
Passo 1
Nesse exercício vamos utilizar a equação para o mínimo de difração e as relações trigonométricas para estabelecer conexões entre a distância do máximo central e a distância entre os mínimos de difração.
Passo 2
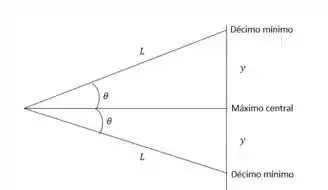
Temos que pela simetria do problema, precisaremos calcular apenas e multiplicar por 2, pois a distância entre os mínimos até o máximo central são iguais. Podemos estabelecer uma relação trigonométrica para a partir do seno, onde
Mas temos também que para um mínimo, a equação que mostra sua posição é
Assim, se substituirmos da primeira relação na segunda, chegaremos na seguinte equação
Calculando então para, chegamos que será
Multiplicando esse valor por 2, vamos chegar que a distância entre os dois mínimos será de .
Resposta
.