Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 31

Em suas férias nas montanhas, você faz uma caminhada. De manhã, seu deslocamento é S → m a n h ã = 2.000   m ,   l e s t e + 3.000   m ,   n o r t e + ( 200   m ,   v e r t i c a l ) . Depois do almoço, seu deslocamento é S → t a r d e = ( 1.500   m ,   o e s t e ) + ( 2.000   m ,   n o r t e ) - ( 300   m ,   v e r t i c a l ) .

  1. Ao final da caminhada, a que altura acima ou abaixo você se encontra do ponto de partida?
  2. Qual é o modulo de seu deslocamento resultante neste dia?

Passo 1

O sistema de coordenadas ( x ,   y ,   z )   é mostrado aqui. Enquanto +   x indica leste e +   y indica norte, a direção   +   z está verticalmente para cima.

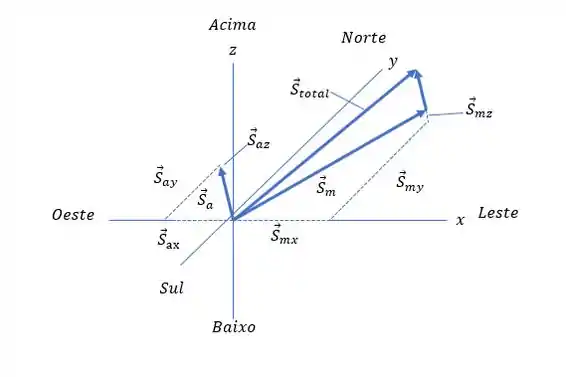
Os vetores mostrados estão representado da seguinte maneira: S → m a n h ã = S → m S → t a r d e = S → a .

E o vetor total do deslocamento: S → t o t a l = S → a + S → m (também é mostrado).

Passo 2

S → m é dado por:

S → m = 2000 i ^ + 3000 j ^ + 200 k ^ m

e

S → a = - 1500 i ^ + 2000 j ^ - 300 k ^ m .

O deslocamento total é a soma dos deslocamentos individuais. 

Passo 3

  1. A soma dos componentes   z dos deslocamentos da tarde e da manhã é

    2. S z a + S a m = - 300 m + 200 m = - 100 m ,

    isto é, 100   m abaixo.

    Passo 4

  2. E S → t o t a l = S → a + S → m é:

S → t o t a l = 500 i ^ + 5000 j ^ - 100 k ^ m ,

ou seja, ( 500   m   l e s t e ) + ( 5000   m   n o r t e ) - ( 100   m   n a   v e r t i c a l ) . A magnitude do seu deslocamento total é

S t o t a l = 500 2 + 5000 2 + - 100 2 m = 5,03   k m

Resposta

  1. 100   m abaixo
  2. S t o t a l = 5,03   k m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o produto vetorial, prove a lei dos senos para o triângulo mostrado na figura 10-43. Isto é, se A ,B e C são comprimentos de cada lado do triângulo, mostre que A s e n a = B s e n b = C s e n c
Para os vetores A→ e B → incicados na Fígura 1.34 use diagramas em escala para determinar a) a soma vetorial A → + B → b) a diferença vetorial A → – B → . Use suas respostas para encontrar o módulo e
Determine o módulo, a direção e o sentido dos vetores representados pelos seguintes pares de componentes: a) A x = - 8,60 c m ,A y = 5,20c m ; b) A x = - 9,70m ,A y = - 2,45m ; c) A x = 7,75 k m ,A y
Para os vetores A →eB → , indicados na Figura 1.34, use o métododos componentes para determinar o módulo, a direção e o sentidoa) da soma vetorialA → +B → b) da soma vetorial B→ + A → c) da diferença
Seja A → = 5 i ^ + 2 j ^ e B → = - 3 i ^ - 5 j ^ e C → = A → + B → Expresse o vetor C → em termos de componentes.Desenhe um sistema de coordenadas e sobre ele represente os vetores A → , B → e C → .Qu