Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 36
Usando o produto vetorial, prove a lei dos senos para o triângulo mostrado na figura 10-43. Isto é, se e são comprimentos de cada lado do triângulo, mostre que .
Passo 1
Representando com vetores, temos:
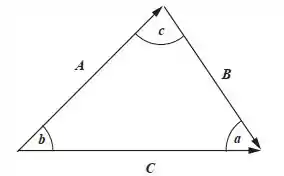
Repare que podemos escrever o seguinte: .
Passo 2
Como ele falou para usarmos produto vetorial, lá vamos nós:
Além disso,
Como :
Passo 3
Finalizando:
Aplicando modulo dos dois lados:
Substituindo as coisas,
Do mesmo jeito, podemos achar que:
Portanto,
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A FIGURA P3.28 mostra os vetores A → e B → . Encontre D → = 2 A → + B → .Expresse sua resposta em termos dos componentes.
A FIGURA P3.27 mostra os vetores A → e B → . Encontre o vetor tal que A → + B → + C → = 0 → . Expresse sua resposta em termos dos componentes.
Em suas férias nas montanhas, você faz uma caminhada. De manhã, seu deslocamento é S → m a n h ã = 2.000m ,l e s t e + 3.000m ,n o r t e + ( 200m ,v e r t i c a l ) ã . Depois do almoço, seu deslocame
Bob caminha 200 m para o sul, depois troteia 400 m para o sudoeste e finalmente caminha 200m na direção 30 ° a leste de norte.a. Trace uma representação gráfica acurada do movimento de Bob. Use régua
A Figura PO1.13 mostra dois vetores D 1 → e D 2 → . Qual das possibilidades de (a) a (d) é o vetor D 2 → - 2 D 1 → , ou (e) nenhuma delas?