Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.8 - Ex. 39
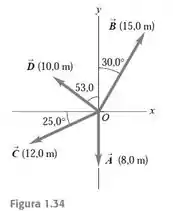
Para os vetores , indicados na Figura 1.34, use o métododos componentes para determinar o módulo, a direção e o sentido
a) da soma vetorial
b) da soma vetorial
c) da diferença vetorial
d) da diferença vetorial
Passo 1
Fala aí! tudo certinho? 😬
Nesse problema foi dado dois vetores e nosso objetivo é fazer algumas operações entre eles...
Vamos analisar a questão:
Se , pelo método das componentes, sabemos que: e .
Pela figura, temos que:
e
E para o vetor
Veja só! 😇
Passo 2
- , então, sabemos que
- Quando somamos, não importa a ordem, teremos o mesmo resultado, certo? Aqui em vetores não é diferente:
- Se , então, sabemos que:
E
Para definirmos a direção, vamos calcular:
Tranquilo até aqui? 😉
Passo 3
Então sabemos que o modulo dessa soma vetorial é e direção .
Bacana, não é? 👀
Passo 4
E
E para definirmos a direção:
Estamos quase lá! 😁
Passo 3
Para o item d), temos , porem sabemos que
Então sabemos que o modulo dessa diferença vetorial é de e direção .
E fim! O que achou? Responde Aí! 😎
Resposta
- e
- e
- e
- e