Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 46

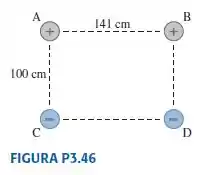
A FIGURA P3.46 mostra quatro cargas elétricas localizadas nas arestas de um retângulo. Como você deve saber, cargas de mesmo sinal se repelem, enquanto cargas de sinais opostos se atraem. A carga B exerce uma força repulsiva de 3,0 N (apontando diretamente para fora de B) sobre a carga A. A carga C exerce uma força atrativa de 6,0 N (apontando diretamente para C) sobre a carga A. Finalmente, a carga D exerce uma força atrativa de 2,0 N sobre a carga A. Considerando as forças como vetores, qual é o módulo e qual é a orientação da força resultante F → r e s exercida sobre a carga A?

Passo 1

Bom galera, primeiro vamos visualizar melhor:

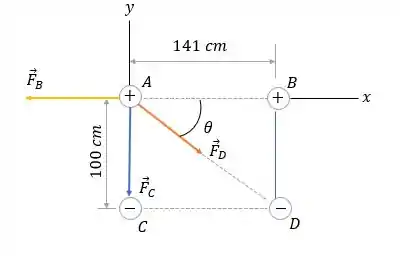
Nós conhecemos F B = 3   N F C = 6   N F D = 2   N , e queremos encontrar F → t o t a l . Então, vamos lá.

Passo 2

Usando trigonometria para calcular θ , obtemos:

θ = tan - 1 ⁡ 100 c m 141 c m = 35,3 ° .

Passo 3

Expressando as três forças em vetores unitários,

F → B = - 3   N   i ^ , F → C = - 6   N   j ^ ,

e F → D = + 2   N cos ⁡ 35,3 °   i ^ - 2   N s e n   35,3   j ^ = 1,63   N i ^ - 1,16   N j ^ .

Passo 4

A força total é:

F → t o t a l = F → B + F → C + F → D = - 1,37   N   i ^ - 7,2   N   j ^ .

A magnitude de F → t o t a l é

F t o t a l = 1,63   N 2 + 7,2 N 2   = 7,3   N

E o ângulo é dado por:

θ t o t a l = tan - 1 ⁡ F t o t a l y F t o t a l x = tan - 1 ⁡ 7,2   N 1,37   N = 79 °  

Resposta

F → t o t a l = 7,3   N , 79   ° abaixo de −x no quadrante III

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A aceleração de uma partícula é dada por a x ( t ) = - 2,0m / s + ( 3,0m / s 3 ) t . a) Calcule a velocidade inicial v 0 x de modo que a partícula tenha a mesma coordenada x para t = 0 s e t = 4 s . b
Se um objeto está se movendo em uma linha reta com aceleração constante, sua velocidade instantânea no meio de um intervalo de tempo qualquer é (a) maior do que a sua velocidade média, (b) menor do qu
Em uma corrida, em um instante em que dois cavalos estão correndo um ao lado do outro e na mesma direção (a direção + x ), a velocidade e a aceleração instantâneas do cavalo A são + 10m / s e + 2,0m /
A aceleração de uma paraquedista que pula de um avião é dada por a y = g - b v y 2 , onde b é uma constante positiva que depende da área da seção reta da paraquedista e da densidade da atmosfera ao se
Suponha que você conhece os vetores de posição de uma partícula em dois pontos do caminho dela, um anterior ao outro. Você também sabe o tempo que leva para a partícula se mover de um ponto ao outro.