Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.Problemas Adicionais - Ex. 77
Uma roda homogênea de massa e raio está montada rigidamente em um eixo que passa pelo centro (Fig. 11-62). O raio do eixo é e o momento de inércia do conjunto roda-eixo em relação ao eixo é . A roda está inicialmente em repouso no alto de uma superfície que faz um ângulo com a horizontal; o eixo está apoiado na superfície, sem tocá-la. Depois de liberado, o eixo rola para baixo, suavemente e sem deslizamento, ao longo da superfície. Depois que o conjunto roda-eixo desce ao longo da superfície, qual é (a) a energia cinética de rotação e (b) a energia cinética de translação do conjunto?
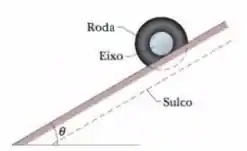
Passo 1
Show de bolinhas pessoal, queremos encontrar encontrar os valores da energia cinética de rotação e da energia cinética de translação , dadas como:
Onde , e são o momento de inércia, a velocidade angular e velocidade linear do conjunto roda-eixo, respectivamente. Agora pra gente conseguir relacionar essas duas energias vamos fazer o seguinte, se liga só:
Inicialmente temos o sistema na configuração inicial dada como na figura abaixo:
Nesse momento inicial o sistema roda-eixo, está momentanemete parado a uma altura do chão:
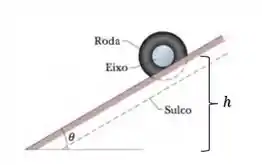
De forma que toda a energia mecânica inicial presente no sistema é formada por energia potencial gravitacional relacionado a altura :
Onde é a massa do conjunto roda-eixo. Agora quando o conjunto roda-eixo percorre uma distância sobre a rampa:
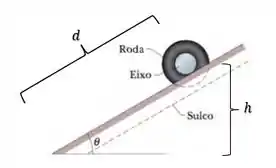
Teremos uma energia mecânica final formada apenas pela energia cinética de rotação e energia cinética de translação , tal que:
A malanadragem agora é a gente lembrar que a energia mecânica desse sistema se conserva, de maneira que:
Passo 2
Iradoso, pra gente conseguir organizar melhor nossa equação, podemos com um pouquinho de trigonometria, descobrir através da figura, que:
Além disso, usando o relação entre a velocidade linear e a velocidade angular para o caso de rolamento sem deslizamento, obtemos:
De maneira que podemos reescrever nossa equação como:
Isolando :
Substituindo os valores dados pelo enunciado, descobrimos que:
Com o valor de no gatilho, podemos determinar a energia cinética de rotação do sistema, de forma que:
Substituindo os valores que descobrimos:
Passo 3
Por fim, usando o vínculo do movimento de translação com o movimento de rotação, temos:
Substituindo os valores:
Assim, calculando a energia cinética de translação:
Tal que:
Resposta
- ;
- .