Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.Problemas Adicionais - Ex. 95
Na Fig. 11-60, uma força horizontal constante de módulo é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é , o raio é e o cilindro rola suavemente em uma superfície horizontal. (a) Qual é o módulo da aceleração do centro de massa do cilindro? (b) Qual é o módulo da aceleração angular do cilindro em relação ao centro de massa? (c) Em termos dos vetores unitários, qual é a força de atrito que age sobre o cilindro?
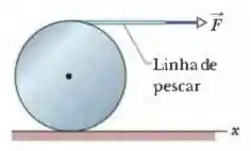
Passo 1
Para questões como essa, devemos lembrar da simplificação que podemos fazer tendo em vista que o ponto de contato do cilindro com o chão está parado, assim, podemos considerar que esteja acontecendo uma rotação pura em torno de um eixo passando pelo ponto de contato entre o chão e o cilindro.
Assim, vamos começar calculando o momento de inércia do sistema em relação ao ponto de contato através do teorema dos eixos paralelo, sabendo que o momento de inércia de um cilindro cujo o eixo de rotação passa pelo seu centro de massa é . Portanto, pelo teorema dos eixos paralelos, temos:
Onde o representa a distância entre os dois eixos, no nosso caso , assim:
Passo 2
Com o momento de inércia em mãos, podemos aplicar a segunda lei de Newton para rotação, sabendo que a única força que realiza torque nessa simplificação é a força :
Como o braço de alavanca da força é , então:
Isolando :
Substituindo os valores:
Passo 3
Com o valor da aceleração angular em mãos, podemos usar a seguinte equação para determinar a aceleração do centro de massa:
Nesse caso, a aceleração que queremos determinar está a uma distância do eixo de rotação, assim:
Passo 4
Para determinar a força de atrito, vamos aplicar a segunda lei de Newton para translação ao eixo horizontal, assim:
Isolando e substituindo os valores, temos:
Resposta
- ;
- ;
- .