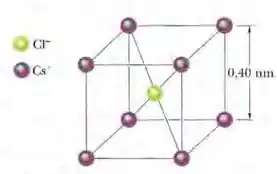
Nos cristais de cloreto de césio, os íons de césio, estão nos oito vértices de um cubo, com um íon de cloro, , no centro (Fig. 21-36). A aresta do cubo tem . Os íons possuem um elétron a menos (e, portanto, uma carga +e) e os íons possuem um elétron a mais (e, portanto, uma carga ) . (a) Qual é o módulo da força eletrostática exercida sobre o íon pelos íons situados nos vértices do cubo? (b) Se um dos íons está faltando, dizemos que o cristal possui um defeito; qual é o módulo da força eletrostática exercida sobre o íon pelos íons restantes?

Como o íon central de está em equilíbrio, a força total sobre ele é nula. Isso por que para cada íon num vértice do cubo tem um outro no vértice oposto que exercem forças que se cancelam. Isso já responde a letra a).

Podemos tambem visualizar de outra forma... perceba que cada cada eixo que atravessa o ion de temos dois ions de em lados opostos, o que acaba anulando as forças. Logo a força resultante no ion é nulo.

Tranquilo até aqui? 😉

Agora, o que acontece com o sistema se, de repente, retiramos um íon de um dos vértices? E aí?

Calma! Você não vai ter que ficar calculando todas as forças que os outros íons césio exercem sobre o íon central. Não queremos ficar a vida toda só fazendo contas, não é mesmo?

Aqui, a gente usa uma ferramenta muito poderosa da física chamada “princípio da superposição”. Nesse caso, a gente pode considerar que o sistema que possui um “buraco” no lugar de um césio é igual à “soma” do sistema original com aquele em que se coloca uma carga em cima desse íon que foi retirado.

Veja só! 😁

Então, fazendo essa artimanha, a gente encontra que a força eletrostática total sobre o íon negativo central é igual à força anterior (nula) somada com a exercida pelo íon , de carga .

Essa força é igual a

em que é metade da diagonal do cubo, dada por

Então:

Aproximadamente.

E aí! entendeu tudo? Responde Aí! 😁