Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.6 - Ex. 27
Um elétron descreve uma trajetória helicoidal em um campo magnético uniforme de módulo . O passo da hélice é e o módulo da força magnética experimentada pelo elétron é . Qual é a velocidade do elétron?
Passo 1
Aqui temos um elétron que faz uma trajetória helicoidal por estar sujeito a um campo magnético e temos que calcular a velocidade do elétron. Olha pra essa imagem aqui embaixo:
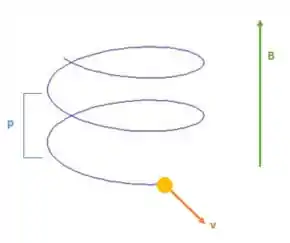
Algumas coisas que temos que reparar:
- Consideramos que o campo está para cima, enquanto o movimento do elétron é helicoidal descendo;
- O passo e
- A velocidade .
Concorda comigo que a distância que um objeto percorre é igual a velocidade multiplicada pelo tempo:
Beleza, bem simples, né? Vamos usar essa ideia aqui também. Olha só, a velocidade pode ser decomposta em duas: uma no eixo e outra no eixo :
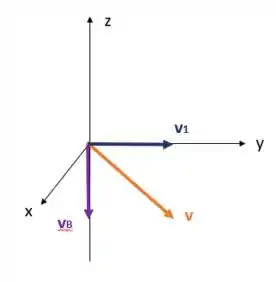
Vamos chamar a velocidade no eixo de e a velocidade no eixo de . Quem ajuda o elétron a fazer o deslocamento paralelo ao campo magnético ?
É a velocidade , sacou o motivo de dar esse nome? Show, então como fica esse deslocamento pra baixo? Já falamos sobre essa fórmula:
Se considerarmos que em um ciclo, a partícula desce o tal do passo que desenhamos na primeira figura:
Assim como a velocidade que contribui para o movimento é . Mas qual é o tempo? Num movimento helicoidal tempo é igual a período:
Ok, vamos substituir na fórmula:
E o período é dado pela equação:
Logo o passo é igual a:
Onde:
- é a massa do elétron:
- é a carga do elétron: (vamos usar o módulo!)
- é o campo elétrico:
- é o passo:
Passo 2
Queremos encontrar a velocidade , logo vamos isolar ela de um lado só:
Substituindo esses valores na equação acima:
Passo 3
Beleza, encontramos uma das componentes de , mas como encontrar ? Pela força aplicada ao elétron! Como assim? Olha pra essa imagem aqui:
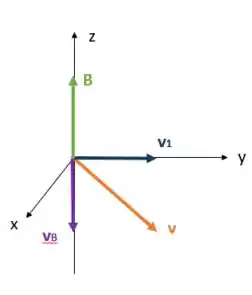
A força é dada pela equação:
Ou seja, é um produto vetorial entre a velocidade e o campo. Como a componente é paralela ao campo magnético, logo ela não produz força, apenas a velocidade . Então:
onde é a velocidade transversal.
Substituindo os valores:
Passo 4
Através do triângulo retângulo formado pelas velocidades, podemos encontrar por:
Substituindo os valores que encontramos: