Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.7 - Ex. 31
Um fio reto longo possui cargas negativas fixas com uma densidade linear de . O fio é envolvido por uma casca coaxial cilíndrica, não condutora, de paredes finas, com de raio . A casca possui uma carga positiva na superfície externa, com uma densidade superficial , que anula o campo elétrico do lado de fora da casca. Determine o valor de .
Passo 1
Lembrando da Lei de Gaus na situação ilustrada, a gente tem que,considerando a superfície pontilhada:
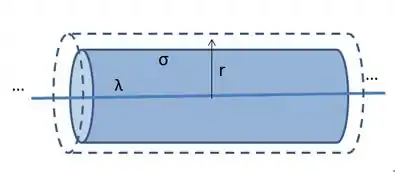
O que deve acontecer para que o campo elétrico seja nulo fora da casca cilíndrica?
Precisamos que o módulo do campo elétrico do cilindro e do fio sejam iguais, pois como o fio possui carga negativa o seu campo será negativo e irá se anular com o campo da casca.
Partindo daqui calcularemos o campo elétrico pro fio e pro cilindro e compararemos ambos, e então será possível encontrar a densidade de cargas.
Passo 2
Para descobrirmos, vamos calcular o campo elétrico devido a cada entidade (fio reto e cilindro que o envolve), a uma distância do eixo do fio:
Já o campo elétrico do cilindro é dado por:
Onde:
E aí a expressão vai ficar:
Agora vamos isolar o campo elétrico do cilindro e a partir disso poderemos relacionar o campo elétrico gerado pelo cilindro com o campo elétrico gerado pelo fio:
Passo 3
Como a gente falou lá no comecinho, pro campo elétrico ser nulo á uma certa distância da casca a seguinte relação deve ser verdade:
Como temos toda a galera é só substituir:
Cortando os termos semelhates temos:
Agora é só isolar e substituir geral!