Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.8 - Ex. 40

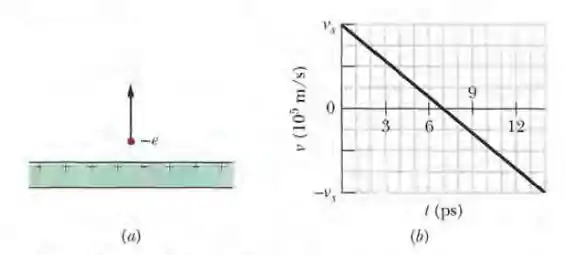
Na Fig. 23-44a, um elétron é arremessado verticalmente para cima, com uma velocidade v s   =   2,0 × 10 5   m / s , a partir das vizinhanças da placa de plástico uniformemente carregada. A placa é não condutora e muito extensa. A Fig. 23-44b mostra a velocidade escalar v em função do tempo t até o elétron voltar ao ponto de partida. Qual é a densidade superficial de cargas da placa?

Passo 1

Primeiramente, vamos nos perguntar: o que a gente consegue extrair do gráfico da Figura (b)?

Veja que a inclinação da reta desse gráfico nos dá a aceleração da partícula!

Então, essa aceleração é igual a:

a = v f - v 0 ∆ t = ( - 2 × 10 5 - 2   × 10 5 )   m / s 14   × 10 - 12   s = - 4   × 10 5 14   × 10 - 12 m / s 2 = - 2,85 × 10 16   m / s 2

Passo 2

Mas como a gente consegue extrair a densidade superficial de cargas dessa aceleração? Como isso nos ajuda?

Conseguiremos isso a partir do cálculo da força resultante:

F = m a = e ⋅ E = e ⋅ σ 2 ϵ 0

Então:

σ = 2 ϵ 0 m a e

A partir dos valores de e = 1,6 × 10 - 19 C , de ϵ 0 = 8,854 × 10 - 12   C 2 / ( N m 2 )   e de m = 9,11 × 10 - 31   k g (a massa do elétron), a gente encontra:

σ = 2 ϵ 0 m a e = 2 ⋅ 8,854 × 10 - 12 ⋅ 9,11 × 10 - 31 ⋅ 2,85   × 10 16 1,6 × 10 - 19

σ = 2,87 × 10 - 6   C m 2

Resposta

σ = 2,87 × 10 - 6   C m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a Qual o excesso de elétrons que deve ser distribuído uniformemente dentro do volume de uma esfera plástica isolada, com 30,0c m de diâmetro, para produzir um campo elétrico de 1150N / C na área exter
Uma única placa condutora isolada (Figura 22.40 ) possui uma carga por unidade de área σ em sua superfície. Como a placa é condutora, o campo elétrico sobre sua superfície é perpendicular ao plano e p
Repita o Problema 22.45 , porém agora supondo que a esfera oca grande possua uma carga igual a - 2 q . Como no Problema 22.45 , a esfera oca pequena continua com uma carga + 2 q .
Uma esfera condutora sólida de raio R possui uma carga positiva Q . A esfera está no interior de uma esfera oca isolante e concêntrica com raio interno R e raio externo 2 R . A esfera isolante possui
Uma carga negativa - Q está distribuída uniformemente sobre uma casca esférica isolante fina, de raio R . Encontre o módulo, a direção e o sentido da força que essa casca esférica exerce sobre uma car