Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 46
Repita o Problema , porém agora supondo que a esfera oca grande possua uma carga igual a . Como no Problema , a esfera oca pequena continua com uma carga .
Passo 1
Para saber o campo elétrico em cada situação, precisamos considerar uma superfície gaussiana adequada para cada uma delas e lembrar da lei de Gauss dada por:
Primeiramente, supondo uma superfície gaussiana esférica de raio , temos que o seu campo elétrico será nulo por não possuir carga em seu interior.
Na região da superfície interna da esfera oca interna, ou seja, em , por se tratar de um condutor carregado, o campo elétrico deve ser nulo.
O mesmo ocorre para , por essa ser a região interna da esfera oca maior que também é um condutor sólido carregado.
Já para a superfície gaussiana de raio , ela envolve a carga da esfera mais interna com valor . Logo, o seu campo elétrico será dado por:
Tomando a superfície de raio , a carga total envolvida por ela é a soma das cargas sobre a esfera mais interna e a externa. Logo, o campo elétrico é:
Passo 2
O gráfico deste caso pode ser dado por:
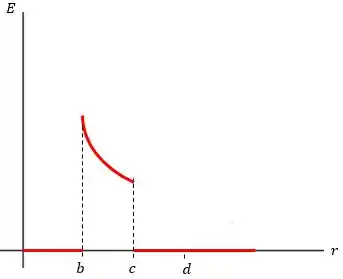
Passo 3
Na região da superfície interna da esfera oca pequena, o campo elétrico deve ser nulo. Por conta disso, o fluxo elétrico também é nulo e, logo, não há carga nessa região.
Agora, para uma superfície gaussiana em , ela envolverá a carga sobre a esfera que tem valor de . Assim, a carga sobre a superfície externa da esfera pequena é .
Da mesma forma, para a superfície interna da esfera oca grande, o campo elétrico em seu interior deve ser nulo. No entanto, como um dos lados dessa esfera oca envolve a carga de da esfera menor, a carga no interior da esfera maior deve ser de mesma intensidade e sinal contrário, ou seja , para que haja “anulação” das cargas e o campo elétrico seja zero.
Para a última região dada por , como a carga no interior da esfera grande é e a carga total sobre ela também é de , podemos concluir que não há carga na superfície externa dessa esfera.