Uma esfera condutora sólida de raio possui uma carga positiva . A esfera está no interior de uma esfera oca isolante e concêntrica com raio interno e raio externo . A esfera isolante possui uma densidade de carga uniforme . Calcule o valor de para que a carga total do sistema seja igual a zero. Usando o valor de encontrado na parte , determine o módulo, a direção e o sentido do campo elétrico em cada uma das regiões , , e . Mostre seus resultados em um gráfico do componente radial em função da distância . Sabemos que, geralmente, o campo elétrico é descontínuo somente através de uma fronteira onde existe uma fina camada de cargas. Explique como seu resultado da parte confirma essa regra.
Passo 1
Para determinarmos o valor da densidade volumétrica de carga, devemos lembrar que ela é dada pela relação entre a carga total do sistema e o seu volume. Como nesse caso temos uma esfera oca, o seu volume é dado por:
Ainda, precisamos lembrar que o campo elétrico no interior de um condutor sólido carregado é nulo.
E, então, considerando uma superfície gaussiana esférica que envolva as esferas, sabemos que devido a esfera condutora, a superfície interna da esfera oca tem carga . Logo, para o campo elétrico em seu interior se manter nulo, a carga no exterior da esfera oca deve ser para se “anular” com a carga positiva já existente.
Dessa forma, a densidade de carga uniforme será dada por:
Passo 2
Para saber o campo elétrico em cada situação, precisamos considerar uma superfície gaussiana adequada para cada uma delas e lembrar da lei de Gauss dada por:
Primeiramente, supondo uma superfície gaussiana esférica de raio , temos que o seu campo elétrico será nulo por não possuir carga em seu interior.
Na região da superfície externa da esfera oca, ou seja, em , como a carga resultante é zero (devido a carga da esfera condutora e da carga no exterior da esfera oca), o campo elétrico também será nulo.
Já para a superfície gaussiana em , ela possui a carga da esfera condutora e a carga proveniente da densidade de carga uniforme da esfera isolante. Logo, o seu campo elétrico será dado por:
Logo:
Agora, substituindo o valor de encontrado antes:
Passo 3
O gráfico deste caso pode ser dado por:
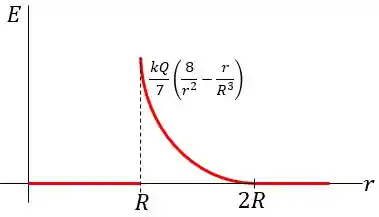
Passo 4
Através do gráfico feito com os valores do campo elétrico nos intervalos dados, podemos observar uma descontinuidade no raio , o pode ser causado pela camada de carga presente na superfície da esfera condutora, onde há a transição dessa esfera para a esfera isolante.