Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Exercício - Ex. 8
As três pequenas esferas indicadas na Figura possuem cargas , e . Determine o fluxo elétrico total através de cada uma das superfícies fechadas cujas seções retas são indicadas na figura: ; ; ; ; . As respostas dos itens de até dependem de como a carga está distribuída em cada esfera pequena? Por quê?
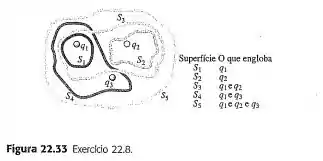
Passo 1
Visto que o cálculo do fluxo elétrico é dado como:
Podemos substituir essas variáveis para atender ao critério de que as cargas são esféricas. Logo:
Então, o fluxo agora é equacionado como:
Assim, como cada esfera gera um campo elétrico sobre a superfície em que se encontra, o fluxo será a soma dos fluxos de cada um desses campos que estiverem em uma determinada área.
Passo 2
Logo, para a superfície :
O mesmo cálculo será feito para cada região. Então para a segunda superfície:
Para :
Para :
E, por fim, para a superfície :
Passo 3
Visto que para esse caso o fluxo depende apenas do valor e sinal da carga na respectiva superfície, é possível dizer que a forma com ela está distribuída não afeta o fluxo elétrico.
Resposta
Não