Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.Problemas Adicionais - Ex. 70
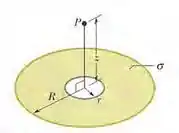
A figura mostra um anel com um raio externo , um raio interno e uma densidade superficial de cargas uniforme . Com no infinito, determine o potencial elétrico no ponto P, situado no eixo central do anel a uma distância do centro do anel.
Passo 1
Antes de iniciarmos esta questão que tal separarmos os dados importantes?
Isso foi necessário porque podemos entender melhor a questão e qual é o melhor método para encontrar o potencial elétrico no ponto P.
Usaremos a seguinte equação aqui para calcular o potêncial elétrico do disco carregado:
Passo 2
Vamos calcular o potencial elétrico do disco, mas há um detalhe importante, temos uma parte em seu centro que temos que retirar da equação. Logo o potencial total será a subtração entre o potencial elétrico do disco de raio pelo potencial do furo no centro de raio .
Onde é o raio maior do disco e é o raio do furo.
Substituindo os dados temos:
E a equação fica:
O potencial elétrico no ponto P é