Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.Problemas Adicionais - Ex. 77

A Fig. 25-58 mostra um circuito com quatro capacitares que está ligado a um circuito maior através dos pontos A e B. As capacitâncias são C 1 = 10 μ F e C 2 = C 3 = C 4 = 20 μ F . A carga do capacitar 1 é 30 μ C . Qual é o valor absoluto da diferença de potencial V A V B ?

Passo 1

Temos um circuito com 4 capacitores de capacitâncias C 1 = 10 μ F e C 2 = C 3 = C 4 = 20 μ F , também sabemos que o capacitor 1 tem carga de q 1 = 30 μ C

Primeiramente, conseguimos observar que os capacitores C 1 e C 2 , estão ligados em paralelo. Portanto, a DDP sobre eles é a mesma, V 1 = V 2 = V 12 , e podemos calcular seu valor pela equação:

V 1 = q 1 C 1

V 1 = 30 × 10 - 6 10 × 10 - 6 = 3,0 V

Além disso, temos que a capacitância equivalente dos dois capacitores ligados em paralelo é:

C 12 = C 1 + C 2

C 12 = 10 + 20 = 30 μ F

Agora, podemos calcular a carga total em cima dos dois capacitores:

q 12 = V 12 C 12

q 12 = 3,0 30 = 90 μ C

Passo 2

Agora, podemos ver também que os capacitores 3 e 4 estão ligados em paralelo e portanto podemos achar uma capacitância equivalente:

C 34 = C 3 + C 4

C 34 = 20 + 20 = 40 μ F

Agora, podemos redesenhar o circuito:

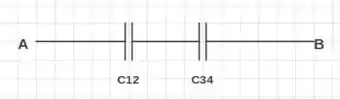Portanto, temos agora que esses dois capacitores estão em série, ou seja, a carga em cima dos dois é igual. Também temos que a DDP total pode ser encontrada com a soma das DDPs de cada capacitor equivalente:

V = V 12 + V 34

V = q 12 C 12 + q 34 C 34 = q 12 1 C 12 + 1 C 34

V = 90 × 10 - 6 1 30 × 10 - 6 + 1 40 × 10 - 6 = 5,3 V

Resposta

V = 5,3 V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois capacitares de placas paralelas, ambos com uma capacitância de 6,0 μ F , são ligados em série a uma bateria de 10 V ; em seguida, a distância entre as placas de um dos capacitares é reduzida à me
Na Fig. 25-56, as placas do capacitor de placas paralelas têm uma área de 2,00 × l 0 - 2 m 2 e o espaço entre as placas é preenchido por dois blocos de material isolante com 2,00 m m de espessura cada
Repita o Problema 67 para os mesmos dois capacitares, supondo que estão ligados em paralelo.
Na Fig. 25-55, V = 12 V , C 1 = C 5 = C 6 = 6,0 μ F e C 2 = C 3 = C 4 = 4,0 μ F . Determine (a) a carga total armazenada nos capacitares; (b) a carga do capacitar C 4 .
Um capacitar de capacitância C 1 = 6,00 μ F é ligado em série com um capacitar de capacitância C 2 = 4,00 μ F e uma diferença de potencial de 200 V é aplicada ao par de capacitares. (a) Calcule a capa