Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 26.4 - Ex. 22
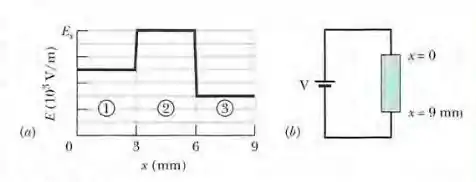
A Fig. 26-24a mostra o módulo do campo elétrico criado por uma bateria ao longo de uma barra resistiva de de comprimento (Fig. 26-24b). A escala vertical é definida por . A barra é formada por três trechos feitos do mesmo material, mas com raios diferentes. (O diagrama esquemático da Fig. 26-24b não mostra os raios diferentes). O raio da seção 3 é . Determine o raio (a) da seção l; (b) da seção 2.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui temos um circuito com uma barra resistiva, que está sendo alimentado por uma bateria. A barra resistiva tem diferentes resistividades dependendo da posição que medimos da barra, já que temos trechos com diâmetros diferentes, teremos que calcular o raio das seções I e II.
Como o material é o mesmo, a resistividade é a mesma, o que significa, de acordo com
a Eq. 26-11, que os campos elétricos nos diferentes trechos são diretamente proporcionais às densidades de corrente.
Passo 2
Temos se os raios de três partes respectivas
Onde
Comprimento do fio
Comprimento de cada seção
Passo 3
A densidade de corrente pode ser expressa em termos do campo elétrico como:
A partir do gráfico, podemos ver que os campos elétricos nas três seções do fio podem ser expressos como:
Portanto, utilizando a equação (1), podemos obter as densidades de corrente correspondentes:
A corrente no fio em todas as seções é a mesma:
onde é a área e é dada por , então:
substitua pelas densidades de corrente para obter:
Se o raio da terceira seção for , o raio das outras seções seria:
Passo 4
(a) O raio da segunda seção é:
Agora para a letra b:
Se o raio da terceira seção é , o raio das outras seções seria:
(b) O raio da primeira seção é: