Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 60

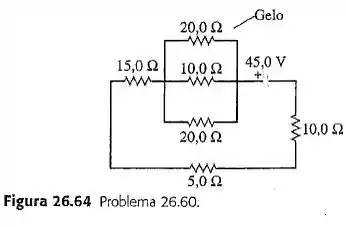
No circuito indicado na Figura 26.64, um resistor de 20,0   Ω está inserido em um grande bloco de gelo 0,0 ° C , e a bateria possui resistência interna desprezível. Qual é a taxa (em g/s) em que esse circuito derreterá o gelo? (O calor latente de fusão para o gelo é de 3,34 × 10 5 J / k g   .)

Passo 1

O calor, gerado no resistor, derrete o gelo.

Bom, encontre a taxa na qual o calor é gerado no resistor 20.0   Ω usando P = V 2 / R . Então use o calor de fusão de gelo para encontrar a velocidade com que o gelo derrete. O calor d H para derreter uma massa de gelo d m é d H = L F d m , onde L F é o calor latente da fusão. A taxa na qual o calor entra no gelo ,   d H / d t , é a potência P no resistor, então P = L F   d m / d t . Portanto, a taxa de derretimento do gelo é d m / d t = P / L F     .

Passo 2

A resistência equivalente do ramo paralelo é de 5,00   Ω , então a resistência total no circuito é de 35,0   Ω . Portanto, a corrente total no circuito é I T o t a l = ( 45,0   V ) / ( 35,0   Ω ) = 1,286   A . A diferença de potencial entre o resistor 20.0 Ω no gelo é o mesmo que a diferença de potencial no ramo paralelo: V g e l o = I T o r a / R p = 1,286   A ) ( 5,00   Ω ) = 6,429   V . A taxa de aquecimento do gelo é P g e l o = V g e l o 2 / R = 6,429   V 2 / ( 20,0   Ω ) = 2,066   W . A energia entra no calor para derreter o gelo, então

d m d t = P L F = ( 2,066 W ) / ( 3,34 × 10 5 J / k g ) = 6,19 × 10 - 6 k g / s = 6,19 × 10 - 3 g / s

Passo 3

A taxa de fusão é de cerca de 6   m g   /   s , o que não é muito. Demoraria 1000   s   para derreter apenas 6   g de gelo.

Resposta

6,19 × 10 - 3 g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois resistores, R1 e R2, podem ser ligados tanto em série quanto em paralelo por meio de uma bateria ideal cuja fem é E. Desejamos que a taxa de dissipação de energia elétrica da combinação em parale
Nove fios de cobre de comprimento l e diâmetro d estão ligados em paralelo formando um único condutor composto de resistência R. Qual deverá ser o diâmetro D de um único fio de cobre de comprimento I,
Dispõe-se de duas baterias de fem E e resistência interna r. Elas podem ser ligadas em paralelo (Fig. 29-29a) ou em série (Fig. 29-29b) e são usadas para estabelecer uma corrente num resistor R. (a) O
A Fig. 29-11a mostra 12 resistores, cada um de resistência R, formando um cubo. (a) Determine Req, a resistência equivalente entre as extremidades da diagonal de uma face. (b) Determine R17, a resistê
(a) Calcule a corrente que atravessa cada uma das baterias ideais da Fig. 29-31. Suponha que R1 = 1,0 Ω, R2 = 2,0 Ω, E1 = 2,0 V e E2 = E3 = 4,0 V. (b) Calcule Va- Vb.