Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.9 - Ex. 24
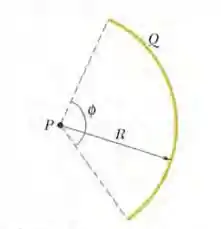
Na figura abaixo, uma barra de plástico com uma carga uniformemente distribuída Q = -25,6 pC tem a forma de um arco de circunferência de raio R = 3,71 cm e ângulo central . Com V = 0 no infinito, qual é o potencial elétrico no ponto P, o centro de curvatura da barra?
Passo 1
Um arco de raio cm, delimitado por um ângulo de , possui uma carga de distribuída uniformemente sobre ele. Precisamos encontrar a diferença de potencial no centro da curvatura.
Vamos calcular o potencial do ponto P pela integral:
Podemos usar essa fórmula? Sim, porque o potencial é 0 no infinito. Mas r é constante (e igual a R), então sai da integral:
Passo 2
Agora é só substituir:
Resposta
Exercícios de Livros Relacionados
Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
(a) A figura (a) mostra uma barra não condutora de comprimento L = 6,00c m e densidade linear de cargas positivas uniforme λ = + 3,68p C / m . Considere V = 0 no infinito. Qual é o valor de V no ponto
Uma distribuição linear de cargas não uniforme dada por λ = b x , onde b é uma constante, está situada no eixo x, entre x=0 e x=0,20m . Se b=20n C / m 2 e V =0 no infinito, determine o potencial elétr
Na Fig. abaixo, três barras finas de plástico têm a forma de quadrantes de circunferência com o mesmo centro de curvatura, situado na origem. As cargas uniformes das barras são Q 1 = +30 nC, Q 2 = +3,
Na Fig. abaixo, determine o potencial elétrico produzido na origem por um arco de circunferência de carga Q 1 = +7,21 pC e duas partículas de cargas Q 2 = 4,00 Q 1 e Q 3 = -2,00 Q 1 . O centro de curv