Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.Problemas Adicionais - Ex. 97

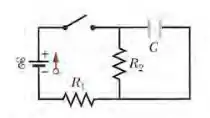
Na Fig. 27-66, a força eletromotriz da fonte ideal é ε = 30 V , as resistências são R 1 = 20 k Ω e R 2 = 10 k Ω e o capacitor está descarregado. Quando a chave é fechada no instante t = 0, determine a corrente (a) na resistência 1 e (b) na resistência 2. (c) Depois de transcorrido um longo tempo, qual é a corrente na resistência 2?

Passo 1

Aqui temos um circuito onde o capacitor está desligado, e fechamos a chave, neste instante de tempo queremos saber a corrente em R 1 e R 2 e para um tempo muito longo a corrente em R 2 .

Passo 2

(a)Como o capacitor está inicialmente descarregado, ele se comporta inicialmente como um curto-circuito e, portanto, a tensão inicial é zero entre os terminais do resistor R 2 e 30 V entre os terminais do resistor R 1 . Assim, de acordo com a lei de Ohm,

i 1 = ε R 1

R 1 = 20 k Ω

ε = 30 V

i 1 = 30 V 20 × 10 3 Ω = 1,5 × 10 3 A = 1,5 m A

Passo 3

Como a tensão inicial entre os terminais do resistor R 2 é 0, i 2 = 0 .

Passo 4

(c) Depois de transcorrido um longo tempo, o capacitor passa a se comportar como um circuito aberto e os resistores R 1 e R 2 passam a se comportar como dois resistores em série, com uma resistência equivalente R e q = R 1 + R 2 = 20 k Ω + 10 k Ω = 30 k Ω . Assim, a corrente no circuito, que é igual à corrente no resistor 2, é

i = ε R e q = 30 V 30 × 10 3 Ω = 1,0 × 10 - 3 A = 1,0 m A

Resposta

(a) i 1 = 1,5 m A

(b) i 2 = 0 .

(c) i = 1,0 m A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A diferença de potencial entre as placas de um capacitor de 2,0 μ F com fuga (o que significa que há uma passagem de carga de uma placa para a outra) diminui para um quarto do valor inicial em 2,0 s .
Um capacitor com uma diferença de potencial inicial de 100 V começa a ser descarregado através de um resistor quando uma chave é fechada no instante t = 0 . No instante t = 10,0 s , a diferença de pot
Um resistor de 15,0 k Ω e um capacitor são ligados em série e uma diferença de potencial de 12,0 V é aplicada bruscamente ao conjunto. A diferença de potencial entre os terminais do capacitor aumenta
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67
A chave S da Fig. 27-63 é fechada no instante t = 0 , fazendo om que um capacitor inicialmente descarregado de capacitância C = 15,0 μ F comece a se carregar através de um resistor de resiscência R =