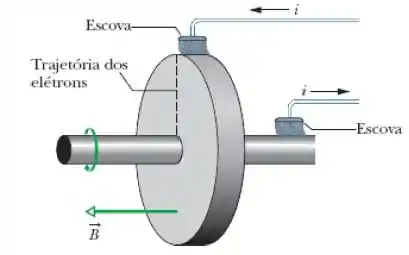
A Fig. 28-56 mostra um gerador homopolar, no qual um motor (que não aparece na figura) faz girar um disco metálico. Duas escovas são usadas para ligar o sistema a um circuito elétrico. Este tipo de gerador pode produzir uma força eletromotriz maior que os geradores que utilizam espiras giratórias, já que o disco pode girar a uma velocidade muito maior que uma espira, sem se romper. Suponha que o disco tem um raio , a frequência da rotação é , e um campo magnético uniforme de módulo é aplicado perpendicularmente ao plano do disco. Quando o disco está girando, os elétrons de condução que estão na reta que liga o eixo do disco a uma das escovas (reta tracejada) são forçados a se mover perpendicularmente ao campo magnético.
(a) Para o sentido de rotação indicado na
figura, os elétrons são submetidos a uma força magnética para cima ou para baixo?
(b) O módulo da força é maior perto da borda ou perto do centro do disco?
(c) Qual é o trabalho por unidade de carga que a força realiza ao longo da reta, do centro até a borda do disco?
 (d) Qual é a diferença de potencial produzida pelo gerador?
(d) Qual é a diferença de potencial produzida pelo gerador?
(e) Se a corrente no circuito é , qual é a potência elétrica produzida pelo gerador?
Passo 1
Letra a:
Usando o sentido da corrente como referência, então sabemos que os elétrons sofrem uma força para cima;
Passo 2
Letra b: e a força é maior perto da borda, pois a força magnética depende da velocidade do portador de carga. Nesse caso a velocidade vai ser , então quanto maior o raio (ou seja maior a distância da carga ao centro do disco) maior a velocidade e consequentemente maior a força.
Passo 3
Letra c:
O trabalho é dado por:
Onde é a força magnética e a distância percorrida que, nesse caso é o próprio raio. Como o deslocamento e a força tem a mesma orientação o ângulo entre eles é zero e . O trabalho então é:
O ângulo entre a força e o campo magnético é , então . O trabalho por unidade de carga vai ser:
Agora vamos substituir a velocidade por que é a velocidade na borda do disco:
E os dados que o problema nos trás são:
Agora é só substituir:
Passo 4
Letra d:
A diferença de potencial é dada pela seguinte expressão:
Passo 5
Letra e:
Potência elétrica é dada pelo produto de por :