Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.9 - Ex. 36
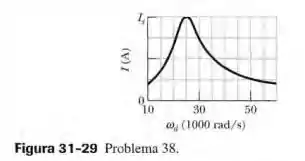
A Fig. 31-29 mostra a amplitude da corrente em função da frequência angular de excitação de um circuito . A escala de eixo vertical é definida por . A indutância é e a amplitude da força eletromotriz é . Determine o valor (a) de e (b) de .
Passo 1
A questão deu a curva de ressonância da corrente em função da frequência angular de excitação. No item (a) ele pede a capacitância do circuito. Para isso, lembre-se que a frequência de ressonância ocorre quando
Assim,
Note que podemos tirar essa frequência do gráfico, basta ver onde ocorre o valor máximo: . Assim, como , temos que
Passo 2
Para calcular a resistência, é só lembrar que
Na ressonância, temos que , de modo que
Portanto, tirando a corrente de ressonância do gráfico, temos que . Portanto, como , temos que