Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.9 - Ex. 51
Na Fig. 31-32, um gerador de frequência ajustável é ligado a um circuito formado pela resistência , as indutâncias e e as capacitâncias , e . (a) Qual é a frequência de ressonância do circuito? Determine o que acontece com a frequência de ressonância (b) quando aumenta; (c) quando aumenta; (d) quando é removido do circuito.
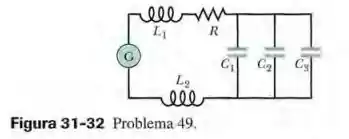
Passo 1
Bom, sabemos que para um circuito com resistência , indutância e capacitância , a frequência angular de ressonância é
Assim,
Mas neste caso, temos mais dois indutores e três capacitores, de modo que temos que calcular a indutância e a capacitância equivalente. Os indutores estão em série, de modo que
Já os capacitores estão em paralelo, de modo que
Passo 2
Portanto, substituindo a indutância equivalente e a capacitância,
Substituindo os valores nas unidades corretas:
Passo 3
Note que não depende de , de modo que se retirarmos o resistor do circuito, a frequência de ressonância não é alterada.
Por outro lado, se aumentar, como ele aparece no denominador de , a frequência deve diminuir.
Por fim, como também aparece no denominador, se ele for retirado a frequência aumenta.
Resposta
Não muda
Diminui
Aumenta