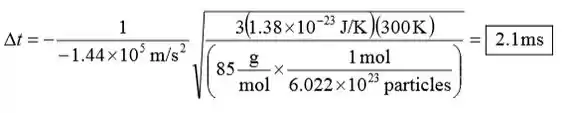Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 30.1 - Ex. 12
No resfriamento e aprisionamento de laser, as forças associadas à pressão de radiação são usadas para diminuir a velocidade dos átomos de centenas de metros por segundo em temperatura ambiente para velocidades de alguns metros por segundo ou mais lentas. Um átomo isolado absorverá apenas radiação de frequências específicas. Se a frequência da radiação do feixe de laser for ajustada de modo que os átomos alvo absorvam a radiação, então a radiação é absorvida durante um processo chamado absorção ressonante. A área da seção transversal do átomo para absorção ressonante é aproximadamente igual a λ 2, onde λ é o comprimento de onda da luz laser. (a) Estime a aceleração de um átomo de rubídio (massa molar 85 g / mol) em um feixe de laser cujo comprimento de onda é 780 nm e intensidade é 10 W / m2. (b) Quanto tempo levaria para tal feixe de luz reduzir a velocidade de um átomo de rubídio em um gás à temperatura ambiente (300 K) até a velocidade próxima de zero?
Passo 1
Fala galera, tudo bem? Vamos que vamos! Podemos usar a segunda lei de Newton para expressar a aceleração de um átomo em termos da força resultante agindo sobre o átomo e a relação entre a pressão de radiação e a intensidade do feixe para encontrar a força resultante. Uma vez que conhecemos a aceleração de um átomo, podemos usar a definição de aceleração para encontrar o tempo de parada de um átomo de rubídio à temperatura ambiente.
Passo 2
(a) Aplique a segunda lei de Newton ao átomo para obter:
A pressão de radiação Pr e a intensidade do feixe I estão relacionadas de acordo com:
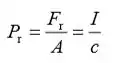
Resolva para Fr para obter:
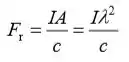
Substitua Fr na equação (1) para obter:
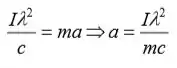
Substitua os valores numéricos e avalie a:
Passo 3
(b) Usando a definição de aceleração, expresse o tempo de parada Δt do átomo:
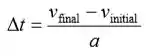
Porque v final ≈ 0:
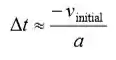
Usando a velocidade rms como a velocidade inicial de um átomo, relacione v inicial à temperatura do gás:
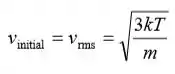
Substitua na expressão o tempo de parada para obter:
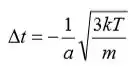
Substitua os valores numéricos e avalie o Δt:
