Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.4 - Ex. 3
Quais são (a) a componente e (b) a componente de um vetor do plano que faz um ângulo de no sentido anti-horário com o semieixo positivo e tem um módulo de ?
Passo 1
Fala galera, tudo certo? Bem, a questão quer as componentes de um vetor. Qual melhor forma de achar elas se não desenhar esse vetor primeiro? Sabemos que ele:
- É um vetor () do plano
- Faz um ângulo de no sentido anti-horário com o semieixo positivo
- Tem um módulo de
A terceira informação por enquanto não vamos precisar, mas com as duas primeiras, conseguimos desenhar:
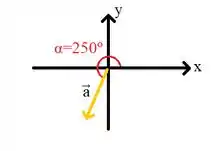
Show de bola. Agora saca só o seguinte. Vamos chamar esse ângulo aqui de :
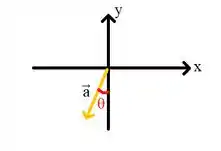
E vamos calcular esse cara! Como o ângulo abaixo é de :
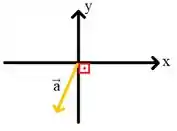
Temos que:
Passo 2
Ta, beleza, mas como isso ajuda? Calma gafanhoto. Lembra dessa imagem?
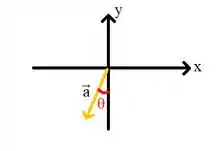
Que tal projetar a ponta desse vetor nos eixos? Vamos ter:
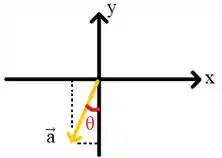
O que nos permite destacar um triângulo muito bacana:
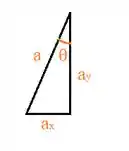
E ajeitando ele pra ficar mais fácil de visualizar as coisas:
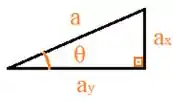
E pronto! Temos tudo pra achar as componentes que queremos! Utilizando a definição do seno:
Isolando :
Substituindo os valores :
Seguindo o mesmo raciocínio, porém usando a definição de cosseno:
Isolando o :
Só lembra o seguinte galera, esses são os módulos das componentes, mas como o vetor está no terceiro quadrante, pra expressar os vetores e , devemos considerar a direção e sentido negativas dos vetores: