Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.4 - Ex. 42
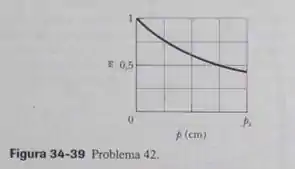
Um objeto é colocado no centro de uma lente delgada e deslocado ao longo do eixo central. Durante o movimento, a ampliação lateral é medida. A Fig. 34-39 mostra o resultado em função da distância do objeto até . Determina a ampliação lateral para .
Passo 1
Bom, a equação dá para gente vários valores de e de conforme o gráfico. Vamos usar a equação de ampliação:
Como também varia junto com quando a gente muda , precisamos fazer o sumir, para isso vamos combinar essa equação com a equação de lentes delgadas:
Assim, some, e aparece , mas ele não varia, o que resolve o nosso problema de duas variáveis.
Isolando na equação de lentes:
E substituindo na equação de ampliação:
Passo 2
Agora olhando pro gráfico, a gente pode ver que , quando , substituindo esses valores na equação que a gente deduziu no passo 1, ficamos com:
Isolando :
Passo 3
Agora que sabemos , podemos substituir o dado no enunciado para acharmos o que corresponde a ele: