Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.Problemas - Ex. 47
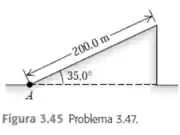
Um foguete de teste é lançado por aceleração ao longo de uma inclinação de , a , partindo do repouso no ponto (Figura ). A inclinação se ergue a sobre a horizontal e, no instante em que o foguete parte dela, os motores se apagam e ele fica sujeito somente à gravidade (a resistência ao ar pode ser desprezada). Determine
a) a altura máxima sobre o solo atingida pelo foguete e
b) o maior alcance horizontal do foguete passando-se o ponto .
Passo 1
Fala, querido!
Vamos entender o que está acontecendo? O foguete é lançado por essa plataforma inclinada com aceleração . Aí depois que ele sai dessa plataforma, essa aceleração para de atuar.
Em outras palavras, até ele sair da plataforma temos um movimento uniformemente variado na direção da plataforma e depois a gente tem um lançamento de projétil. Ou seja, a velocidade final do MRUV vai ser a velocidade inicial do projetil.
Vamos achar essa para a plataforma usando Torricelli, sabendo que a velocidade inicial para essa parte do movimento é nula ().
Substituindo os valores:
E essa vai ser o módulo da velocidade inicial (fim da rampa) que vamos usar a seguir. Repara que ela vai estar inclinada de em relação a horizontal como a rampa.
Agora nosso problema vira um lançamento de projétil. Ele pede a altura e o alcance máximo. Vamos achar essas grandezas. Atenção que ele pede em relação ao solo (para a altura) e em relação a (para o alcance).
Vamos considerar para cima e origem do referencial em , porque ele quer as grandezas em relação a esse ponto (que está no solo).
Vamos lá!
Passo 2
- Para determinar a altura máxima precisamos determinar a equação de movimento na vertical. A componente vertical da velocidade inicial é:
- Para determinar o alcance, precisamos determinar o tempo que o foguete permanece no ar. Da equação vertical temos:
E usando a equação de movimento
Lembrando que na altura máxima a velocidade é zero, pois saindo da plataforma, ele para de acelerar e vai perdendo velocidade:
A altura inicial é a altura da rampa (onde começa o movimento de projeto). Podemos acha-la, assim:
Voltando para a nossa equação do movimento,
Tranquilo até aqui?
Passo 3
Temos a velocidade inicial. A posição inicial já vimos que é . A posição final é o solo, então . A aceleração é a da gravidade .
Substituindo os valores teremos uma equação de segunda ordem em :
Usando Bhaskara temos as raízes:
E como só a raiz positiva nos interessa:
Show?
Passo 3
Agora que temos o tempo, vamos substituir na expressão pra posição horizontal. A componente horizontal da velocidade inicial é:
e lembrando que na horizontal não temos mais aceleração, então é um MRU. A posição inicial é quando a acaba a rampa. Em relação a , tendo como referência zero:
Assim a posição em é:
Obs: Ficamos beeem diferentes do gabarito. Mas isso ocorre porque essa edição tem um problema de tradução. A aceleração do foguete na rampa é dada como e o gabarito considera como .
Se você seguir esse passo a passo, apenas mudando a aceleração inicial do foguete para , cê chega no gabarito do livro, tá bem?
E fim! Entendeu tudo? Responde Aí!
