Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 39.3 - Ex. 19

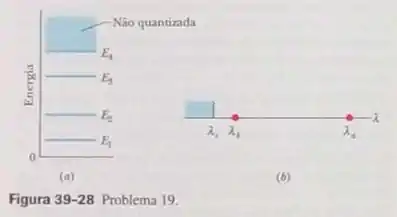
A Fig. 39-28a mostra o diagrama de níveis de energia de um poço de potencial unidimensional finito que contém um elétron. A região não quantizada começa em . A Fig. 39-28b mostra o espectro de absorção do elétron quando se encontra no estado fundamental. O elétron pode absorver fótons com os comprimentos de onda indicados: , e qualquer comprimento de onda menor que . Qual é a energia do primeiro estado excitado?

Passo 1

Bom, podemos escrever a energia associada a cada comprimento de onda que foi dado no enunciado, para isso, basta pegarmos a equação:

E substituir a frequência através da equação da velocidade da luz no vácuo:

Ficando com:

Passo 2

Para os três comprimentos de onda a gente vai ter as seguintes energias:

Como é constante, escrevemos ela em termos de :

Ficando o seguinte:

E as outras energias vão ser:

Passo 3

Como o comprimento que tem a maior energia, é o comprimento , e pela figura, ele está associado ao nível (para a esquerda na figura (b) a escala fica azul, o que significa que dali para frente, a energia não está mais quantizada), podemos calcular a energia do estado fundamental fazendo a subtração:

Isolando :

Passo 4

E ela figura de novo, está mais para a direita, sendo a menor energia que o elétron pode absorver para subir para um estado excitado, como é a menor, ela tá associada ao estado . Então a gente faz o mesmo que fizemos para encontrar a energia do estado fundamental no passo 3:

Isolando :

E essa é a energia para o estado .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Como sugere a figura 39-8, a densidade de probabilidade na região xL do poço de potencial finito da figura 39-7 diminui exponencialmente, de acordo com a equação ψ 2 x = C e - 2 k x , onde C é uma con

Um eletrôn. no estado n = 2 do poço de potencial finito da Fig. 39-7 absorve uma energia de 400e V de uma fonte externa. Use o diagrama de níveis de energia da Fig. 39-9 para determinar a energia ciné

A Fig. 39-29a mostra um tubo fino no qual foi montado um poço de potencial finito, com V 2 = 0 . Um elétron se move para a direita no interior do poço, em uma região onde a tensão é V 1 = - 9,00V , co

A Fig. 39-9 mostra os níveis de energia de um elétron confinado em um poço de potencial finito com 450e V de profundidade. Se o elétron se encontra no estado n = 3 , qual é a sua energia cinética?

( a ) Mostre que para a região xL do poço de potencial finito da Fig. 39-7, ψ x = D e 2 k x , é uma solução da equação de Schrödinger unidimensional, onde D é uma constante e k é um número real positi