Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 63
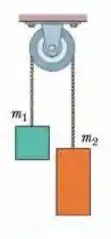
A Fig. 5-47 mostra uma máquina de Atwood, na qual dois recipientes estão ligados por uma corda (de massa desprezível) que passa por uma polia sem atrito (também de massa desprezível). No instante , o recipiente tem uma massa de e o recipiente tem uma massa de , mas o recipiente está perdendo massa (por causa de um vazamento) a uma taxa constante de . Com que taxa o módulo da aceleração dos recipientes está variando (a) em e (b) em ? (c) Em que instante a aceleração atinge o valor máximo?
Passo 1
Esta é uma questão não muito comum em física I, pois envolve a aplicação da segunda lei de Newton para um corpo cuja a massa varia com o tempo.
Para ser uma resolução mais visual, vamos proceder de modo análogo ao que fazemos com as massas fixas. Para tanto, vamos iniciar escrevendo a segunda lei de Newton para o eixo de cada bloco individualmente:
Bloco :
Bloco :
Vamos, começar a entender essas equações... Primeiro, por que eu usei nas duas? As trações que atuam nos blocos têm o mesmo módulo, tendo em vista que a polia é ideal. Nós sabemos que as acelerações de cada bloco também têm o mesmo módulo, porque os blocos se movem juntos. Por fim, como determinei o semieixo positivo apontando para cima, no qual um bloco sobe e outro desce, então eu tive que expressar qual sobe e qual desce no sinal de mais e de menos do lado direito da equação da segunda lei de Newton. Pegou?
Passo 2
Agora isolaremos a tração na :
Substituindo na ;
Isolando o :
Passo 3
Antes de substituir os valores dados no problema, precisamos lembrar que tem uma peculiaridade, então vamos transcrever o que foi dado no problema de forma numérica:
Ou seja, inicialmente tem massa igual a , porém a cada segundo ela perde .
Passo 4
Substituindo os valores na :
Passo 5
Com a função da aceleração calculada, podemos determinar com que taxa o módulo da aceleração está variando nos instantes pedido derivando esta função. Para isso, teremos que usar a regra do quociente:
Passo 6
Para o instante de :
Passo 7
Para o instante :
Passo 8
Para determinar a aceleração máxima, poderíamos pensar nos pontos críticos da derivada e blá blá blá, porém, segue meu raciocínio:
Eu tenho dois blocos, onde um está caindo e outro está subindo. O bloco que está caindo só não está em queda livre devido a tração que liga os dois corpos, pois o segundo bloco, apesar de estar subindo, ele tem a força peso vertical e para baixo. Show? Então, pensando nesse sistema a massa do bloco que está caindo vai ser máxima quando a massa do bloco que está subindo e perdendo massa for zero.
Assim:
Isolando o :
Resposta
- ;
- ;
- .