Você está trabalhando para uma revista automotiva e está avaliando um automóvel novo (massa 650 kg) através de seus ritmos. Enquanto está sendo acelerado a partir do repouso, o seu computador de bordo registra sua velocidade como função do tempo da seguinte forma:

(a) Usando uma planilha eletrônica, encontre a aceleração média dos cinco intervalos de tempo e plote a velocidade versus tempo e aceleração versus tempo para este carro. (b) Onde, no gráfico de velocidade versus tempo, a força resultante no carro é máxima e mínima? Explique seu raciocínio. (c) Qual é a força resultante média sobre o carro durante todo o trajeto? (d) A partir do gráfico de velocidade versus tempo, faça uma estimativa da distância total coberta pelo carro.
Passo 1
Item (a)
Bem, para essa questão, utilizamos um programa de criação de planilha (pode ser o Excel, LibreOffice entre outras opções). Para utilizar o Excel, é necessário um pouco de conhecimento sobre ele, porém não iremos aprofundar na utilização desse programa. O que faremos nessa planilha poderíamos fazer apenas utilizando uma calculadora.
Primeiro, criamos uma planilha e colocamos a massa de na cédula da planilha. Na coluna , colocamos os tempos, como são 6 tempos, colocamos da cédula até a cédula . Na coluna colocamos as velocidades, como são 6 também, colocamos da cédula até a cédula . Assim, podemos calcular a variação média de tempo fazendo a diferença entre duas cédulas de tempo próximas (lembrando que a variação de tempo é sempre positiva) e podemos calcular a aceleração fazendo
Podemos calcular a força também, fazendo os valores de força encontrados estão nas cédulas até e a força média está na cédula .
Então, a tabela que construímos foi esta:
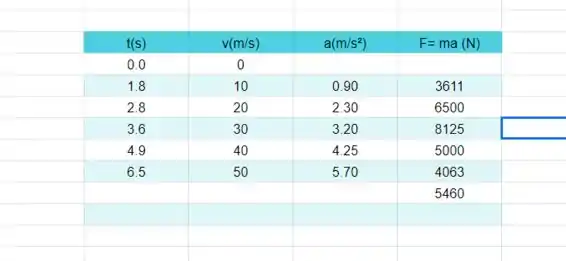
Passo 2
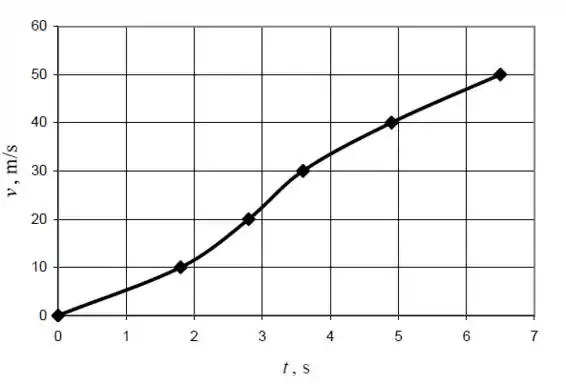
Neste mesmo programa de criação de planilhas, podemos gerar um gráfico de velocidade por tempo. O gráfico que nós geramos está abaixo:
E também, conseguimos gerar um gráfico de aceleração por tempo:
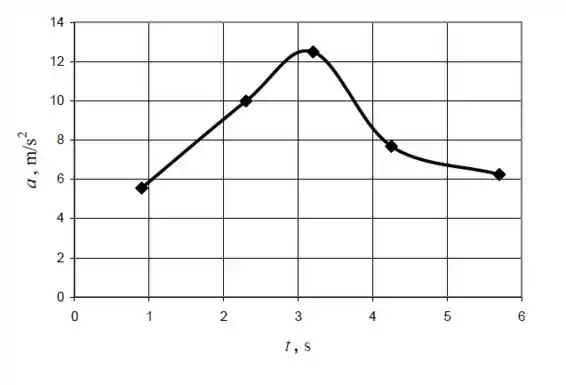
Passo 3
Item (b)
Nós podemos ver no gráfico de velocidade por tempo que quando a linha tem uma inclinação maior é quando a aceleração é maior, o que faz sentido, já que uma inclinação maior significa uma variação maior da velocidade em um intervalo menor de tempo, que é medida pela aceleração. A inclinação é maior entre os pontos de velocidade e , isto é, entre os tempos e . E a aceleração é mínima nos pontos que apresentam uma menor inclinação, que são os pontos onde a velocidade é e , isto é, entre os tempos e .
Passo 4
Item (c)
A força resultante média já foi calculada no item (a) 😊, basta que a gente calcule a força a cada intervalo de dois valores de tempo (através da fórmula ) e a gente soma todos os 5 valores encontrados e divide por 5, fazendo, assim, a média
Passo 5
Item (d)
Uma das formas mais simples de se fazer estimativa é calcular a área debaixo do gráfico de velocidade por tempo, já que a distância percorrida em que é a base do triângulo e é a altura. Então,
Resposta
(b) Maior aceleração entre os tempos e e menor aceleração entre os tempos e .
(c)
(d)