Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.Problemas Adicionais - Ex. 71
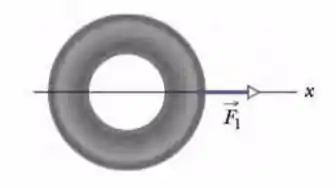
A Fig. 5-62 é uma vista superior de um pneu de que está sendo puxado por três cordas horizontais. A força de uma das cordas () está indicada. As outras duas forças devem ser orientadas de tal forma que o módulo da aceleração do pneu seja o menor possível. Qual é o menor valor de se (a) , ; (b) , ; (c) ?
Passo 1
Vamos começar analisando o primeiro caso. Neste se a gente somar o módulo dos vetores e obtemos o valor do módulo do vetor :
A partir dessa observação, podemos afirmar que o menor possível devemos colocar os vetores e na mesma direção do vetor , porém em sentidos opostos. Dessa forma:
Substituindo os valores e isolando o :
Passo 2
Para o segundo caso, faremos de maneira análoga:
Como a soma dos módulos dos dois vetores acima é menor do que o módulo do vetor sabemos que não conseguiremos ter uma aceleração nula, porém ao colocar ambos na mesma direção de no sentido contrário, conseguidos determinar a menor aceleração possível:
Substituindo os valores e isolando :
Passo 3
Para o último caso, ao somarmos o módulo dos vetores percebemos que este é maior do que o módulo do vetor . Como os dois vetores tem o mesmo módulo, podemos estabelecer um ângulo no segundo e no terceiro quadrante de forma que a soma das componentes do eixo sejam iguais a e a soma da componentes no eixo desses dois vetores se cancelem. Ficou um pouco difícil de visualizar, né? Mas dá uma olhadinha nessa ilustração para ver se melhora:
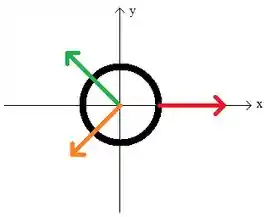
Ao colocarmos ambos os vetores que possuem o mesmo módulo com a mesma angulação partindo do eixo conseguimos o que falamos acima e, portanto, conseguimos a aceleração nula, pois a soma vetorial desses vetores será zero.
Resposta
- ;
- ;
- .